सर्वांगसमता
| ज्यामिति |
|---|
 ओक्सीरिंकस पेपिरस(P.Oxy. I 29) जो यूक्लिड का एलीमेंट्स का एक टुकड़ा दिखा रहा है |
| ज्यामिति का इतिहास |
|
अनुसंधान के क्षेत्रों |
|
महत्वपूर्ण अवधारणा बिंदु · सरल रेखा · Perpendicular · Parallel · Line segment · Ray · समतल · लम्बाई · क्षेत्रफल · आयतन · Vertex · कोण · सर्वांगसमता · समरूपता · बहुभुज · त्रिभुज · Altitude · Hypotenuse · पायथोगोरस प्रमेय · चतुर्भुज · Trapezoid · Kite · Parallelogram (Rhomboid, आयत, Rhombus, वर्ग) · Diagonal · सममिति · वक्र · वृत्त · Area of a disk · Circumference · Diameter · Cylinder · Sphere · पिरामिड आकार · आयाम (एक, दो, तीन, चार) |
|
रेखागणितज्ञ आर्यभट · Ahmes · एपोलोनियस · आर्किमिडिज़ · बौधायन · ब्रह्मगुप्त · यूक्लिड · पाइथागोरस · खय्याम · देकार्त · पास्कल · ओइलर · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · कात्यायन · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · पांकरे · Sijzi · हिल्बर्ट · Minkowski · Cartan · Veblen · Sakabe Kōhan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng |

ज्यामिति में बिन्दुओं के दो समुच्चय को परस्पर सर्वांगसम (congruent) कहते हैं यदि उनमें से किसी एक समुच्चय को स्थानान्तरण (translation),घूर्णन (rotation), परावर्तन (reflection) या इनके मिश्रित क्रियाओं के द्वारा परिवर्तित करने पर दूसरा समुच्चय प्राप्त किया जा सके। सर्वांगसम = सर्व + अंग + सम = सभी अंग बराबर। इसे और अधिक सरल रूप में यों कह सकते हैं कि दो चित्र यदि आकार-प्रकार (shape and size) में समान हैं तो वे परस्पर सर्वांगसम होते हैं (यद्यपि वे अलग-अलग स्थान पर हैं या अलग-अलग स्थितिओं में हो सकते हैं)।
त्रिभुजों की सर्वांगसमता[संपादित करें]

यदि दो त्रिभुजों की तीनों भुजायें एवं संगत कोण समान हों तो वे परस्पर सर्वांगसम होते हैं।
किन्तु प्रायः केवल तीन संगत अंगों की समानता प्रदर्शित कर देना ही सर्वांगसमता सिद्द करने के लिये पर्याप्त होता है।
SAS, SSS, ASA, एवं AAS[संपादित करें]
- SAS (भुजा-कोण-भुजा): यदि दो त्रिभुजों की दो संगत भुजाएँ और उनके बीच के कोण समान हों तो वे सर्वांगसम हैं।
- SSS (भुजा-भुजा-भुजा): यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों संगत भुजों के बराबर हों तो दोनो त्रिभुज सर्वांगसम हैं।
- ASA (कोण-भुजा-कोण): यदि संगत कोणों का एक युग्म और उनकी सम्मिलित भुजा बराबर हो तो दोनो त्रिभुज सर्वांगसम हैं। ASA अभिधारणा का योगदान थेल्स ऑफ मिलेटस (ग्रीक) द्वारा किया गया था।
- AAS (कोण-कोण-भुजा): यदि दो त्रिभुजों के कोणों के दो युग्म माप में बराबर हों, और संगत गैर-शामिल भुजाओं का एक युग्म लंबाई में बराबर हो, तो त्रिभुज सर्वांगसम होते हैं। एएएस एक एएसए शर्त के बराबर है, इस तथ्य से कि यदि कोई दो कोण दिए गए हैं, तो तीसरा कोण भी प्राप्त किया जा सकता, क्योंकि उनका योग 180° होना चाहिए।
- RHS (समकोण-कर्ण-पक्ष): यदि दो समकोण त्रिभुजों के कर्णों की लंबाई समान है, और छोटी भुजाओं का एक युग्म लंबाई में समान है, तlokesh bhambhu Nyolakhi
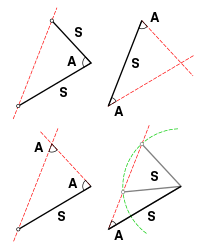
=== SSA: सर्वांगसमता की संदिग्ध स्थिति = कोण (जिसे ASS (एंगल-साइड-साइड) के रूप में भी जाना जाता है) को निर्दिष्ट करती है, हमेशा सर्वांगसमता साबित नहीं होती है।
विशेष रूप से, SSA तब सर्वांगसमता सिद्ध नहीं करता है जब कोण न्यून हो और विपरीत भुजा आसन्न भुजा से छोटी या बराबर हो, लेकिन आसन्न भुजा के कोण के ज्या से अधिक लंबी हो। यह अस्पष्ट मामला है। अन्य सभी मामलों में, SSA सर्वांगसमता सिद्ध करता है। ध्यान दें कि विपरीत पक्ष कोण की ज्या के आसन्न पक्ष से छोटा नहीं हो सकता क्योंकि यह त्रिभुज का वर्णन नहीं कर सकता है।
यदि कोण अधिक या सम हो तो SSA स्थिति सर्वांगसमता सिद्ध करती है। समकोण के मामले में (जिसे HL (हाइपोटेन्यूज़-लेग) स्थिति के रूप में भी जाना जाता है), हम तीसरे पक्ष की गणना कर सकते हैं और SSS पर वापस आ सकते हैं।
SSA स्थिति सर्वांगसमता सिद्ध करती है यदि कोण न्यून हो और विपरीत भुजा या तो आसन्न भुजा को कोण की ज्या (समकोण त्रिभुज) के गुणा के बराबर हो या आसन्न भुजा से लंबी हो।
AAA[संपादित करें]
AAA (कोण-कोण-कोण) इस स्थिति में दोनो त्रिभुज केवल समरूप होते हैं, जरूरी नहीं कि वे सर्वांगसम भी हों। ऐसा इसलिये है कि यह स्थिति आकार (size) के बारे में कुछ भी नहीं कहती। तथापि
इन्हें भी देखें[संपादित करें]
बाहरी कड़ियाँ[संपादित करें]
- The SSS
- The SSA
- Interactive animations demonstrating Congruent angles, Congruent line segments, Congruent triangles, Congruent polygons
