तीन रेखाओं के समीकरण तथा ग्राफ : लाल रेखा तथा नीली रेखा परस्पर समानान्तर हैं। सरल रेखा गणित में शून्य चौड़ाई वाला अनन्त लम्बाई वाला एक आदर्श वक्र होता है, यूक्लिडीय ज्यामिति (Euclidean Geometry) के अन्तर्गत दो बिन्दुओं से होकर एक और केवल एक ही रेखा जा सकती है। एक सरल रेखा दो बिदुओं के बीच की लघतुत्तम दूरी प्रदर्शित करती है। सरल रेखा बिन्दुओं का सरलतम बिन्दुपथ होता है।
किसी द्वी-विमीय समतल पर दो सरल रेखाएं या तो समानान्तर होंगी अथवा प्रतिछेदी। इसी प्रकार त्रिविम में दो रेखाएं परस्पर समानान्तर, प्रतिछेदी या skew (न प्रतिछेदी न ही समानान्तर) हो सकती हैं।
विभिन्न पद्धतियों में सरल रेखा [ संपादित करें ] एक ही सरल रेखा को तीन अलग-अलग रूपों वाले समीकरणों से निरूपित किया गया है:
y
=
k
x
+
b
,
x
a
+
y
b
=
1
{\displaystyle \scriptstyle {y=kx+b,\;{\frac {x}{a}}+{\frac {y}{b}}=1}}
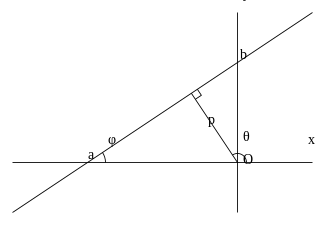
x
cos
θ
+
y
sin
θ
−
p
=
0
{\displaystyle \scriptstyle {x\cos \theta +y\sin \theta -p=0}}
बिन्दु
P
0
(
x
0
|
y
0
)
{\displaystyle P_{0}(x_{0}|y_{0})}
α
{\displaystyle \alpha }
y
=
y
0
+
tan
(
α
)
⋅
(
x
−
x
0
)
{\displaystyle y=y_{0}+\tan(\alpha )\cdot (x-x_{0})}
उपरोक्त समीकरण को निम्नलिखित ढंग से भी लिख सकते हैं (m को रेखा की प्रवणता (स्लोप) कहते हैं)।
y
=
y
0
+
m
⋅
(
x
−
x
0
)
{\displaystyle y=y_{0}+m\cdot (x-x_{0})}
उदाहरण बिन्दु
A
=
(
−
5
,
3
)
{\displaystyle A=(-5,3)}
m
=
2
{\displaystyle m=2}
y
−
y
0
=
m
(
x
−
x
0
)
{\displaystyle y-y_{0}=m(x-x_{0})\!}
y
−
3
=
2
(
x
−
(
−
5
)
)
{\displaystyle y-3=2(x-(-5))\!}
y
−
3
=
2
(
x
+
5
)
{\displaystyle y-3=2(x+5)\!}
y
−
3
=
2
x
+
10
{\displaystyle y-3=2x+10\!}
y
−
2
x
−
3
−
10
=
0
{\displaystyle y-2x-3-10=0\!}
y
−
2
x
−
13
=
0
{\displaystyle y-2x-13=0\!}
दो बिन्दुओं
P
1
(
x
1
|
y
1
)
{\displaystyle P_{1}(x_{1}|y_{1})}
P
2
(
x
2
|
y
2
)
{\displaystyle P_{2}(x_{2}|y_{2})}
x
1
≠
x
2
{\displaystyle x_{1}\neq x_{2}}
y
=
y
1
+
y
2
−
y
1
x
2
−
x
1
⋅
(
x
−
x
1
)
{\displaystyle y=y_{1}+{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot (x-x_{1})}
इसी को इस प्रकार भी लिख सकते हैं-
y
=
y
1
x
−
x
2
x
1
−
x
2
+
y
2
x
−
x
1
x
2
−
x
1
{\displaystyle y=y_{1}{\frac {x-x_{2}}{x_{1}-x_{2}}}+y_{2}{\frac {x-x_{1}}{x_{2}-x_{1}}}}
इसी को सारणिक (डिटर्मिनैन्ट) के रूप में निम्नलिखित प्रकार से लिखा जा सकता है-
|
x
y
1
x
1
y
1
1
x
2
y
2
1
|
=
0
{\displaystyle {\begin{vmatrix}x&y&1\\x_{1}&y_{1}&1\\x_{2}&y_{2}&1\end{vmatrix}}=0}
यदि कोई रेखा x अक्ष पर
a
{\displaystyle a}
b
{\displaystyle b}
x
a
+
y
b
=
1
{\displaystyle {\frac {x}{a}}+{\frac {y}{b}}=1\!}
सरल रेखा का सामान्य समीकरण (general equation):
A
x
+
B
y
+
C
=
0
{\displaystyle Ax+By+C=0\!}
A
,
B
,
C
∈
R
{\displaystyle A,B,C\in \mathbb {R} \!}
B
≠
0
{\displaystyle B\neq 0\!}
[1] प्राचल के रूप (parametric form) में-
{
x
=
x
0
+
a
x
t
,
y
=
y
0
+
a
y
t
,
{\displaystyle {\begin{cases}x=x_{0}+a_{x}t,\\y=y_{0}+a_{y}t,\end{cases}}}
ध्रुवीय निर्देशांक (r , θ ) , और कार्तीय निर्देशांक में सम्बन्ध निम्नलिखित समीकरणों से दर्शाया जा सकता है-
x
=
r
cos
θ
,
y
=
r
sin
θ
.
{\displaystyle x=r\cos \theta ,\quad y=r\sin \theta .}
अतः यदि कोई रेखा मूल बिन्दु (0, 0) से होकर नहीं जाती तो उसका ध्रुवीय समीकरण निम्नलिखित होगा-
r
=
p
cos
(
θ
−
φ
)
,
{\displaystyle r={\frac {p}{\cos(\theta -\varphi )}},}
जहाँ r > 0
φ
−
π
/
2
<
θ
<
φ
+
π
/
2.
{\displaystyle \varphi -\pi /2<\theta <\varphi +\pi /2.}
p उस रेखा की मूल बिन्दु से दूरी (सदा धनात्मक) और
φ
{\displaystyle \varphi }
यदि कोई रेखा
r
→
0
,
{\displaystyle {\vec {r}}_{0},}
u
→
.
{\displaystyle {\vec {u}}.}
r
→
=
r
0
→
+
t
u
→
.
{\displaystyle {\vec {r}}={\vec {r_{0}}}+t{\vec {u}}.}
जहाँ
t
{\displaystyle t}
स्पेस में किसी बिन्दु
(
x
1
,
y
1
,
z
1
)
{\displaystyle (x_{1},\;y_{1},\;z_{1})}
{
x
=
x
0
+
t
α
,
y
=
y
0
+
t
β
,
t
∈
R
z
=
z
0
+
t
γ
,
{\displaystyle {\begin{cases}x=x_{0}+t\alpha ,\\y=y_{0}+t\beta ,\quad t\in \mathbb {R} \\z=z_{0}+t\gamma ,\end{cases}}}
वास्तव में, त्रिबिम स्पेस में सरल रेखा को दो समतलों के प्रतिच्छेद के रूप में देखा जाता है। अतः निम्नलिखित दो समीकरण सम्मिलित रूप से एक रेखा के समीकरण हैं-
3 चरों में दो एकघातीय समीकरण
{
x
+
y
+
z
=
4
x
−
y
+
3
z
=
7
{\displaystyle \left\{{\begin{matrix}x&+y&+z&=4\\x&-y&+3z&=7\end{matrix}}\right.}
वास्तव में उपरोक्त दो समीकरण आलग-अलग दो समतलों को निरूपित करते हैं।
↑ Geometría Analítica ( 1980) Charles Lehmann; Editorial Limusa, ISBN 968-18-176-3; pg. 65