"सर्वांगसमता": अवतरणों में अंतर
No edit summary |
छो Bot: अंगराग परिवर्तन |
||
| पंक्ति 1: | पंक्ति 1: | ||
{{ज्यामिति}} |
{{ज्यामिति}} |
||
[[ |
[[चित्र:Congruence.png|thumb|350px| '''सर्वांगसमता''' का एक उदाहरण - वायीं तरफ् की दो आकृतियाँ सर्वांगसम हैं; तीसरी आकृति उनके [[समरूप]] है; अन्तिम आकृति, पहली दो आकृतियों के '''न''' तो सर्वांगसम है न ही समरूप।]] |
||
[[ज्यामिति]] में बिन्दुओं के दो समुच्चय को परस्पर '''सर्वांगसम''' (congruent) |
[[ज्यामिति]] में बिन्दुओं के दो समुच्चय को परस्पर '''सर्वांगसम''' (congruent) कहते हैं यदि उनमें से किसी एक समुच्चय को स्थानान्तरण (translation), [[घूर्णन]] (rotation), परावर्तन (reflection) या इनके मिश्रित क्रियाओं के द्वारा परिवर्तित करने पर दूसरा समुच्चय प्राप्त किया जा सके। सर्वांगसम = सर्व + अंग + सम = सभी अंग बराबर । इसे और अधिक सरल रूप में यों कह सकते हैं कि दो चित्र यदि आकार-प्रकार (shape and size) में समान हैं तो वे परस्पर सर्वांगसम होते हैं (यद्यपि वे अलग-अलग स्थान पर हैं या अलग-अलग स्थितिओं में हो सकते हैं) । |
||
==त्रिभुजों की सर्वांगसमता== |
== त्रिभुजों की सर्वांगसमता == |
||
[[चित्र:Equiv1.PNG|thumb|right|300px|त्रिभुजों के सर्वांगसम होने की विभिन्न दशाएँ]] |
[[चित्र:Equiv1.PNG|thumb|right|300px|त्रिभुजों के सर्वांगसम होने की विभिन्न दशाएँ]] |
||
[[ |
[[चित्र:Congruent triangles.svg|thumb|200px|right| दो त्रिभुज सर्वांगसम हो सकते हैं यदि - दोनो की दो भुजायें एवं उनके बीच का कोण समान हों (SAS); कोई दो कोण एवं उनके बीच की भुजा समान हों (ASA) या दो कोण एवं इनमें किसी एक से संलग्न भुजा समान हो (AAS). किन्तु दो भुजाएं एवं तीसरी भुजा से संलग्न कोई कोण समान होने की स्थिति में (SSA), प्रायः दो भिन्न-भिन्न त्रिभुज सम्भव हैं]] |
||
यदि दो त्रिभुजों की तीनों भुजायें |
यदि दो त्रिभुजों की तीनों भुजायें एवं संगत कोण समान हों तो वे परस्पर '''सर्वांगसम''' होते हैं। |
||
किन्तु प्रायः केवल तीन संगत अंगों |
किन्तु प्रायः केवल तीन संगत अंगों की समानता प्रदर्शित कर देना ही सर्वांगसमता सिद्द करने के लिये पर्याप्त होता है। |
||
===SAS, SSS, ASA, एवं AAS=== |
=== SAS, SSS, ASA, एवं AAS === |
||
'''SAS (भुजा-कोण-भुजा)''': यदि दो त्रिभुजों की दो संगत भुजाएँ और उनके बीच के कोण समान हों तो वे सर्वांगसम हैं। |
'''SAS (भुजा-कोण-भुजा)''': यदि दो त्रिभुजों की दो संगत भुजाएँ और उनके बीच के कोण समान हों तो वे सर्वांगसम हैं। |
||
| पंक्ति 20: | पंक्ति 20: | ||
'''ASA (कोण-भुजा-कोण)''': Two triangles are congruent if a pair of corresponding angles and the included side are equal. |
'''ASA (कोण-भुजा-कोण)''': Two triangles are congruent if a pair of corresponding angles and the included side are equal. |
||
The ASA Postulate was contributed by Thales of Miletus (Greek). |
The ASA Postulate was contributed by Thales of Miletus (Greek). |
||
In most system of axioms, the three criteria — '''SAS''', '''SSS''' and '''ASA''' — are established as [[theorem]]s. In the [[School Mathematics Study Group]] system '''SAS''' is taken as one (#15) of 22 postulates. |
In most system of axioms, the three criteria — '''SAS''', '''SSS''' and '''ASA''' — are established as [[theorem]]s. In the [[School Mathematics Study Group]] system '''SAS''' is taken as one (#15) of 22 postulates. |
||
| पंक्ति 26: | पंक्ति 26: | ||
'''AAS (कोण-कोण-भुजा)''': Two triangles are congruent if a pair of corresponding angles and a not-included side are equal, since the 3rd angle would have to be equal, and therefore the side would be included. This one is valid only in Euclidean geometry. |
'''AAS (कोण-कोण-भुजा)''': Two triangles are congruent if a pair of corresponding angles and a not-included side are equal, since the 3rd angle would have to be equal, and therefore the side would be included. This one is valid only in Euclidean geometry. |
||
===SSA: सर्वांगसमता की संदिग्ध स्थिति === |
=== SSA: सर्वांगसमता की संदिग्ध स्थिति === |
||
The '''SSA''' condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as '''ASS''' (Angle-Side-Side)) does not always prove congruence. |
The '''SSA''' condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as '''ASS''' (Angle-Side-Side)) does not always prove congruence. |
||
| पंक्ति 35: | पंक्ति 35: | ||
The '''SSA''' condition proves congruence if the angle is acute and the opposite side either equals the adjacent side times the sine of the angle (right triangle) or is longer than the adjacent side. |
The '''SSA''' condition proves congruence if the angle is acute and the opposite side either equals the adjacent side times the sine of the angle (right triangle) or is longer than the adjacent side. |
||
===AAA=== |
=== AAA === |
||
'''AAA''' (कोण-कोण-कोण) इस स्थिति में दोनो त्रिभुज केवल [[समरूप]] होते हैं, जरूरी नहीं कि वे सर्वांगसम भी हों। ऐसा इसलिये है कि यह स्थिति आकार (size) के बारे में कुछ भी नहीं कहती। तथापि यदि गोलीय (spherical) ज्यामिति या अतिपरवलीय (hyperbolic) ज्यामिति की बात करें तो उनमें यह स्थिति सर्वांगसमता के लिये पर्याप्त है। |
'''AAA''' (कोण-कोण-कोण) इस स्थिति में दोनो त्रिभुज केवल [[समरूप]] होते हैं, जरूरी नहीं कि वे सर्वांगसम भी हों। ऐसा इसलिये है कि यह स्थिति आकार (size) के बारे में कुछ भी नहीं कहती। तथापि यदि गोलीय (spherical) ज्यामिति या अतिपरवलीय (hyperbolic) ज्यामिति की बात करें तो उनमें यह स्थिति सर्वांगसमता के लिये पर्याप्त है। |
||
==इन्हें भी देखें== |
== इन्हें भी देखें == |
||
*[[समरूपता]] |
* [[समरूपता]] |
||
==वाह्य सूत्र== |
== वाह्य सूत्र == |
||
*[http://www.cut-the-knot.org/pythagoras/SSS.shtml The SSS] |
* [http://www.cut-the-knot.org/pythagoras/SSS.shtml The SSS] |
||
*[http://www.cut-the-knot.org/pythagoras/SSA.shtml The SSA] |
* [http://www.cut-the-knot.org/pythagoras/SSA.shtml The SSA] |
||
*Interactive animations demonstrating [http://www.mathopenref.com/congruentangles.html Congruent angles], [http://www.mathopenref.com/congruentlines.html Congruent line segments], [http://www.mathopenref.com/congruenttriangles.html Congruent triangles], [http://www.mathopenref.com/congruentpolygons.html Congruent polygons] |
* Interactive animations demonstrating [http://www.mathopenref.com/congruentangles.html Congruent angles], [http://www.mathopenref.com/congruentlines.html Congruent line segments], [http://www.mathopenref.com/congruenttriangles.html Congruent triangles], [http://www.mathopenref.com/congruentpolygons.html Congruent polygons] |
||
[[श्रेणी:ज्यामिति]] |
[[श्रेणी:ज्यामिति]] |
||
13:25, 14 फ़रवरी 2013 का अवतरण
| ज्यामिति |
|---|
 ओक्सीरिंकस पेपिरस(P.Oxy. I 29) जो यूक्लिड का एलीमेंट्स का एक टुकड़ा दिखा रहा है |
| ज्यामिति का इतिहास |
|
अनुसंधान के क्षेत्रों |
|
महत्वपूर्ण अवधारणा बिंदु · सरल रेखा · Perpendicular · Parallel · Line segment · Ray · समतल · लम्बाई · क्षेत्रफल · आयतन · Vertex · कोण · सर्वांगसमता · समरूपता · बहुभुज · त्रिभुज · Altitude · Hypotenuse · पायथोगोरस प्रमेय · चतुर्भुज · Trapezoid · Kite · Parallelogram (Rhomboid, आयत, Rhombus, वर्ग) · Diagonal · सममिति · वक्र · वृत्त · Area of a disk · Circumference · Diameter · Cylinder · Sphere · पिरामिड आकार · आयाम (एक, दो, तीन, चार) |
|
रेखागणितज्ञ आर्यभट · Ahmes · एपोलोनियस · आर्किमिडिज़ · बौधायन · ब्रह्मगुप्त · यूक्लिड · पाइथागोरस · खय्याम · देकार्त · पास्कल · ओइलर · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · कात्यायन · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · पांकरे · Sijzi · हिल्बर्ट · Minkowski · Cartan · Veblen · Sakabe Kōhan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng |

ज्यामिति में बिन्दुओं के दो समुच्चय को परस्पर सर्वांगसम (congruent) कहते हैं यदि उनमें से किसी एक समुच्चय को स्थानान्तरण (translation), घूर्णन (rotation), परावर्तन (reflection) या इनके मिश्रित क्रियाओं के द्वारा परिवर्तित करने पर दूसरा समुच्चय प्राप्त किया जा सके। सर्वांगसम = सर्व + अंग + सम = सभी अंग बराबर । इसे और अधिक सरल रूप में यों कह सकते हैं कि दो चित्र यदि आकार-प्रकार (shape and size) में समान हैं तो वे परस्पर सर्वांगसम होते हैं (यद्यपि वे अलग-अलग स्थान पर हैं या अलग-अलग स्थितिओं में हो सकते हैं) ।
त्रिभुजों की सर्वांगसमता

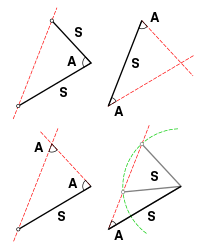
यदि दो त्रिभुजों की तीनों भुजायें एवं संगत कोण समान हों तो वे परस्पर सर्वांगसम होते हैं।
किन्तु प्रायः केवल तीन संगत अंगों की समानता प्रदर्शित कर देना ही सर्वांगसमता सिद्द करने के लिये पर्याप्त होता है।
SAS, SSS, ASA, एवं AAS
SAS (भुजा-कोण-भुजा): यदि दो त्रिभुजों की दो संगत भुजाएँ और उनके बीच के कोण समान हों तो वे सर्वांगसम हैं।
SSS (भुजा-भुजा-भुजा): यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों संगत भुजों के बराबर हों तो दोनो त्रिभुज सर्वांगसम हैं।
ASA (कोण-भुजा-कोण): Two triangles are congruent if a pair of corresponding angles and the included side are equal. The ASA Postulate was contributed by Thales of Miletus (Greek).
In most system of axioms, the three criteria — SAS, SSS and ASA — are established as theorems. In the School Mathematics Study Group system SAS is taken as one (#15) of 22 postulates.
AAS (कोण-कोण-भुजा): Two triangles are congruent if a pair of corresponding angles and a not-included side are equal, since the 3rd angle would have to be equal, and therefore the side would be included. This one is valid only in Euclidean geometry.
SSA: सर्वांगसमता की संदिग्ध स्थिति
The SSA condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as ASS (Angle-Side-Side)) does not always prove congruence.
Specifically, SSA does not prove congruence when the angle is acute and the opposite side is shorter or equal to the adjacent side but longer than the sine of the angle times the adjacent side. This is the ambiguous case. In all other cases, SSA proves congruence. Notice that the opposite side cannot be smaller than the adjacent side times the sine of the angle as this could not describe a triangle.
The SSA condition proves congruence if the angle is obtuse or right. In the case of the right angle (also known as the HL (Hypotenuse-Leg) condition), we can calculate the third side and fall back on SSS.
The SSA condition proves congruence if the angle is acute and the opposite side either equals the adjacent side times the sine of the angle (right triangle) or is longer than the adjacent side.
AAA
AAA (कोण-कोण-कोण) इस स्थिति में दोनो त्रिभुज केवल समरूप होते हैं, जरूरी नहीं कि वे सर्वांगसम भी हों। ऐसा इसलिये है कि यह स्थिति आकार (size) के बारे में कुछ भी नहीं कहती। तथापि यदि गोलीय (spherical) ज्यामिति या अतिपरवलीय (hyperbolic) ज्यामिति की बात करें तो उनमें यह स्थिति सर्वांगसमता के लिये पर्याप्त है।
इन्हें भी देखें
वाह्य सूत्र
- The SSS
- The SSA
- Interactive animations demonstrating Congruent angles, Congruent line segments, Congruent triangles, Congruent polygons
