अपरिमेय संख्या
[गणित] में, अपरिमेय संख्या (irrtional number) वह वास्तविक संख्या है जो परिमेय नहीं है, अर्थात् जिसे भिन्न p /q के रूप में व्यक्त नहीं किया जा सकता है, जहां p और q पूर्णांक हैं, जिसमें q गैर-शून्य है और इसलिए परिमेय संख्या नहीं है। अनौपचारिक रूप से, इसका मतलब है कि एक अपरिमेय संख्या को एक सरल भिन्न के रूप में प्रदर्शित नहीं किया जा सकता। उदाहरण के लिये २ का वर्गमूल, और पाई अपरिमेय संख्याएँ हैं।
यह साबित हो सकता है कि अपरिमेय संख्याएं विशिष्ट रूप से ऐसी वास्तविक संख्याएं हैं जिन्हें समापक या सतत दशमलव के रूप में नहीं दर्शाया जा सकता है, हालांकि गणितज्ञ इसे परिभाषा के रूप में नहीं लेते हैं। कैंटर प्रमाण के परिणामस्वरूप कि वास्तविक संख्याएं अगणनीय हैं (परिमेय गणनीय) यह मानता है कि लगभग सभी वास्तविक संख्याएं अपरिमेय हैं।[1] शायद, सर्वाधिक प्रसिद्ध अपरिमेय संख्याएं हैं π, e और √२.[2][3][4] जब दो रेखा खंडों की लंबाई का अनुपात अपरिमेय है, तो रेखा खण्डों को भी तारतम्यहीन के रूप में वर्णित किया जाता है, वे किसी माप को आम रूप से साझा नहीं करते. इस अर्थ में एक रेखा खंड l का माप एक रेखा खंड J है जिसका "माप" इस अर्थ में l है कि एक छोर से दूसरे छोर तक J की सभी प्रतियों की संख्या 1 के समान ही लंबाई हासिल करती है।
इतिहास[संपादित करें]
अपरिमेयता की अवधारणा को भारतीय गणितज्ञों द्वारा सातवीं शताब्दी ई.पू. से अव्यक्त रूप से स्वीकार किया गया, जब मानव (c. 750-690 ई.पू.) का मानना था कि कुछ विशिष्ट संख्याओं के वर्गमूल जैसे 2 और 61 को निश्चित रूप से निर्धारित नहीं किया जा सकता है।[5]
अपरिमेय संख्या के अस्तित्व के प्रथम सबूत का श्रेय आम तौर पर एक पाईथागोरियाई (संभवतः मेटापोंटम के हिपासस) को दिया जाता है,[6] जिसने शायद पेंटाग्राम के पक्षों की पहचान करने के दौरान उनकी खोज की। [7] उस वक्त के मौजूदा पाइथागोरिआई पद्धति ने दावा किया होता कि वहां जरुर ऐसी कोई पर्याप्त छोटी, अविभाज्य इकाई है जो इन लंबाई में से एक और अन्य में समान रूप से फिट बैठ सकती है। हालांकि, पांचवीं शताब्दी ई.पू. में हिपासस यह परिणाम निकालने में सक्षम था कि वास्तव में मापन की कोई आम इकाई नहीं है और इस तरह के एक अस्तित्व का अभिकथन वास्तव में एक विरोधाभास है। उसने यह प्रदर्शित करते हुए ऐसा किया की वह असंभव है जो यह द्वारा किया प्रदर्शन है कि अगर एक सम त्रिकोण समद्विबाहु का कर्ण वास्तव में एक बाहु से आनुपातिक है, तो माप की उस इकाई को सम और विषम, दोनों होना चाहिए जो कि असंभव है। उसका तर्क इस प्रकार है:
-
- सम त्रिकोण समद्विबाहु की एक बाहु से कर्ण का अनुपात है क्ष:ज्ञ जिसे सर्वाधिक छोटी संभव इकाइयों में व्यक्त किया जाता है।
- पाईथागोरियाई प्रमेय के अनुसार क्ष२ = २ज्ञ२
- चूंकि क्ष२ सम है, क्ष को सम होना होगा क्योंकि विषम संख्या का वर्ग विषम होता है।
- चूंकि क्ष:ज्ञ अपने न्यूनतम मान पर है, तो ज्ञ को विषम ही होना चाहिए.
- चूंकि क्ष सम है, तो मान लेते हैं कि क्ष = २श्र .
- तो क्ष२ = ४श्र२ = २ज्ञ२
- ज्ञ२ = २श्र२ अतः ज्ञ२ को सम ही होना चाहिए, इसलिए ज्ञ भी सम है।
- हालांकि हमने माना कि ज्ञ विषम होना चाहिए. यहीं विरोधाभास है .[8]
यूनानी गणितज्ञों ने असम्मेय परिमाण के इस अनुपात को अलोगोस अथवा वर्णनातीत कहा. हालांकि, उसके प्रयासों के लिए हिपासस की सराहना नहीं की गई: एक कथा के अनुसार, उसने अपनी यह खोज समुद्री यात्रा के दौरान की और उसे बाद में पाईथागोरिआई साथियों द्वारा जहाज से बाहर फेंक दिया गया "...ब्रह्मांड में एक ऐसा तत्त्व उत्पन्न करने के लिए जिसने ... इस सिद्धांत का खंडन किया कि ब्रह्मांड में सभी घटनाओं को पूर्णांक और उनके अनुपात में संक्षिप्त किया जा सकता है।[9] एक अन्य कथा के अनुसार हिपासस को केवल इस रहस्योद्घाटन के लिए निर्वासित कर दिया गया था। हिपासस को खुद जो भी परिणाम भुगतने पड़े हों, उसकी खोज ने पाईथागोरियन गणित के समक्ष एक बहुत गंभीर समस्या खड़ी कर दी, क्योंकि इसने इस धारणा को ध्वस्त कर दिया कि संख्या और ज्यामिति अवियोज्य हैं-उनके सिद्धांत का आधार.
सिरेन के थिओडोरस ने 17 तक के पूर्णाकों के करणीगत की अपरिमेयता को साबित किया, लेकिन वहीं ठहर गया शायद इसलिए क्योंकि जिस बीजगणित का इस्तेमाल उसने किया उसे 17 के वर्ग मूल पर लागू नहीं किया जा सका.[10] और जब युडोक्सस ने अनुपात का सिद्धांत विकसित किया जिसमें अपरिमेय के साथ-साथ परिमेय अनुपात का ध्यान रखा गया, तभी अपरिमेय संख्याओं की मजबूत गणितीय नींव निर्मित हुई.[11] एक परिमाण "एक संख्या नहीं था, बल्कि वह अस्तित्वों के लिए था जैसे रेखा खंड, कोण, क्षेत्र, आयतन और समय जो हम कह सकते हैं लगातार भिन्न हो सकता है। परिमाण, संख्याओं के विपरीत थे, जो एक मान से दूसरे मान में उछल रहे थे, जैसे 4 से 5 पर.[12] संख्याएं कुछ न्यूनतम, अविभाज्य इकाई से बनी होती हैं, जबकि परिमाण अपरिमित रूप से कम करने योग्य हैं। क्योंकि परिमाण के लिए कोई मात्रात्मक मूल्यों को नहीं सौंपा गया था, इसलिए युडोक्सस, सम्मेय और असम्मेय, दोनों अनुपातों की गणना करने में सक्षम हुआ जिसके लिए उसने एक अनुपात को उसके परिमाण और समानुपात के मामले में दोनों अनुपातों के बीच एक समानता के रूप में परिभाषित किया। समीकरण से मात्रात्मक मानों (संख्या) को बाहर लेते हुए, उसने एक अपरिमेय संख्या को एक संख्या के रूप में व्यक्त करने के जाल से खुद को बचाया. "युडोक्सस सिद्धांत ने असम्मेय अनुपातों के लिए आवश्यक परिमेय आधार प्रदान करते हुए यूनानी गणितज्ञों को ज्यामिति में अभूतपूर्व प्रगति करने में सक्षम बनाया."[13] यूक्लिड की एलिमेंट्स पुस्तक 10, अपरिमेय परिमाण के वर्गीकरण को समर्पित है।
मध्य युग[संपादित करें]
मध्य युग में, अरब गणितज्ञों द्वारा बीजगणित के विकास ने अपरिमेय संख्याओं को "बीजीय वस्तुओं" के रूप में प्रयोग करने की अनुमति दी। [14] अरब गणितज्ञों ने, "संख्या" और "परिमाण" की अवधारणा को "वास्तविक संख्या" की एक अधिक सामान्य धारणा में विलय भी किया, यूक्लिड के अनुपात की अवधारणा की आलोचना की, समग्र अनुपात के सिद्धांत का विकास किया और संख्या की अवधारणा को सतत परिमाण के अनुपात तक विस्तारित किया।[15] एलिमेंट्स की पुस्तक 10 पर अपनी टिप्पणी में फारसी गणितज्ञ अल महनी (d. 874/884) ने द्विघात अपरिमेय और घन अपरिमेय की जांच की और उनका वर्गीकरण किया। उसने परिमेय और अपरिमेय परिमाण के लिए परिभाषा प्रदान की, जिसे वह अपरिमेय संख्या के रूप में मानता था। उसने उनका इस्तेमाल मुक्त रूप से किया लेकिन उनकी व्याख्या ज्यामितीय शब्दों में की जो निम्नानुसार है:[16]
"It will be a rational (magnitude) when we, for instance, say 10, 12, 3%, 6%, etc., because its value is pronounced and expressed quantitatively. What is not rational is irrational and it is impossible to pronounce and represent its value quantitatively. For example: the roots of numbers such as 10, 15, 20 which are not squares, the sides of numbers which are not cubes etc."
रेखाओं के रूप में परिमाण की यूक्लिड की अवधारणा के विपरीत, अल-महनी ने पूर्णांक और भिन्न को परिमेय परिमाण के रूप में माना और वर्ग मूल और घन मूल को अपरिमेय परिमाण के रूप में. उसने अपरिमेयता की अवधारणा के लिए एक अंकगणितीय दृष्टिकोण भी पेश किया, जैसा की वह निम्नलिखित का श्रेय अपरिमेय परिमाण को देता है:[16]
"their sums or differences, or results of their addition to a rational magnitude, or results of subtracting a magnitude of this kind from an irrational one, or of a rational magnitude from it."
मिस्र का गणितज्ञ अबू कामिल शुजा इब्न असलम (c. 850-930) प्रथम व्यक्ति था जिसने अपरिमेय संख्याओं को द्विघात समीकरण के समाधान के रूप में या एक समीकरण में गुणांक के रूप में स्वीकार किया, जो अक्सर वर्ग मूल, घन मूल और चौथे मूल के स्वरूप में होता था।[17] दसवीं शताब्दी में, इराकी गणितज्ञ अल-हाशिमी ने गुणन, भाग और अन्य अंकगणितीय क्रियाओं पर विचार करने की प्रक्रिया में अपरिमेय संख्याओं के लिए सामान्य (ज्यामितीय प्रदर्शनों के बजाय) सबूत प्रदान किये। [18] अबू ज़फर अल खज़ीन (900-971), परिमेय और अपरिमेय परिमाण परिभाषा प्रदान करता है, यह कहते हुए कि यदि एक निश्चित राशि है:[19]
"contained in a certain given magnitude once or many times, then this (given) magnitude corresponds to a rational number. . . . Each time when this (latter) magnitude comprises a half, or a third, or a quarter of the given magnitude (of the unit), or, compared with (the unit), comprises three, five, or three fifths, it is a rational magnitude. And, in general, each magnitude that corresponds to this magnitude (i.e. to the unit), as one number to another, is rational. If, however, a magnitude cannot be represented as a multiple, a part (l/n), or parts (m/n) of a given magnitude, it is irrational, i.e. it cannot be expressed other than by means of roots."
इन अवधारणाओं को फलस्वरूप 12वीं सदी के लैटिन अनुवाद के कुछ समय बाद यूरोपीय गणितज्ञों द्वारा स्वीकार कर लिया गया। 12वीं सदी के दौरान मघरेब (उत्तरी अफ्रीका) का एक अरबी गणितज्ञ, अल हस्सार जो इस्लामिक उत्तराधिकार न्यायशास्त्र में विशेषज्ञ था, उसने भिन्न के लिए आधुनिक प्रतीकात्मक गणितीय अंकन विकसित किया, जहां गणक और हर को एक क्षैतिज रोध द्वारा पृथक किया जाता है। यही समान भिन्नात्मक संकेतन शीघ्र ही 13वीं सदी में फिबोनैकी के कार्यों में प्रकट होता है। [उद्धरण चाहिए] 14वीं से 16वीं शताब्दी के दौरान, संगमग्राम के माधव और खगोल विज्ञान और गणित के केरल स्कूल ने अपरिमेय संख्याओं के लिए अनंत श्रृंखला की खोज की जैसे pi और त्रिकोणमितीय क्रियाओं के कुछ विशिष्ट अपरिमेय मानों की। ज्येष्ठदेव ने युक्तिभाषा में इन अनंत श्रृंखलाओं के लिए प्रमाण उपलब्ध कराए हैं।[20]
आधुनिक काल[संपादित करें]
17वीं सदी ने, अब्राहम डे मूवर और विशेष रूप से लिओनार्ड युलर के हाथों में काल्पनिक संख्याओं को एक शक्तिशाली उपकरण बनते देखा. उन्नीसवीं शताब्दी में जटिल संख्याओं के सिद्धांत के पूर्ण होने के लिए अपरिमेय का बीजीय और अबीजीय संख्या में विभेदन, अबीजीय संख्या के अस्तित्व का सबूत और अपरिमेय सिद्धांत के वैज्ञानिक अध्ययन का पुनरुत्थान आवश्यक था जिसकी यूक्लिड के बाद से बड़े पैमाने पर उपेक्षा की गई। वर्ष 1872 में कई लोगों ने सिद्धांतों का प्रकाशन किया जिनमें शामिल थे कार्ल विअरस्ट्रास (उनके छात्र कोज़ाक द्वारा), हेन (क्रेल, 74), जोर्ज कैंटर (अन्नालेन, 5) और रिचर्ड डेडेकिंड. 1869 में मेराय ने हेन के समान ही प्रस्थान के समान बिंदु को लिया, लेकिन इस सिद्धांत को आमतौर पर वर्ष 1872 से उद्धृत किया जाता है। विअरस्ट्रास की विधि को 1880 में पूरी तरह से सेल्वाटोर पिंचरले द्वारा आगे बढ़ाया गया,[21] और डेडेकिंड की विधि को लेखक के बाद के कार्यों (1888) और पॉल टेनरी (1894) के समर्थन के माध्यम से अतिरिक्त महत्त्व प्राप्त हुआ। विअरस्ट्रास, कैंटर और हेन ने अपने सिद्धांतों को अनंत शृंखला पर आधारित किया, जबकि डेडेकिंड ने अपने आधारों को वास्तविक संख्या की प्रणाली में एक कटौती (श्निट) की धारणा पर रखा, जिसके तहत उसने सभी परिमेय संख्याओं को विशेष गुणों के आधार पर दो समूहों में विभाजित किया। इस विषय के विकास में बाद में विअरस्ट्रास, क्रोनेकर (क्रेल, 101) और मेराय ने योगदान दिया।
सतत भिन्न, जो अपरिमेय संख्याओं (और केटाल्डी, 1613 के कारण) से नज़दीकी रूप से सम्बंधित हैं उसे युलर के हाथों प्रचार प्राप्त हुआ और उन्नीसवीं शताब्दी की शुरुआत में लग्रांग के लेखन के माध्यम से अधिक उभरा. डिरीचलेट ने भी सामान्य सिद्धांत में अपना योगदान दिया, जैसा कि कई अन्य योगदानकर्ताओं ने इस विषय के अनुप्रयोग के लिए दिया।
लैम्बर्ट (1761) ने साबित किया कि π परिमेय नहीं हो सकता और कहा कि e n तब अपरिमेय होगा जब यदि n परिमेय है (जब तक कि n = 0 ना हो).[22] जबकि लैम्बर्ट के सबूत को अक्सर अधूरा कहा जाता है, आधुनिक आकलन इसे संतोषजनक कह कर समर्थन देता है और वास्तव में अपने समय के लिए यह असामान्य रूप से कठोर है। लीजेंडर (1794) ने, बेसेल-क्लिफर्ड क्रिया पेश करने के बाद, यह दर्शाने के लिए सबूत प्रदान किया π2 अपरिमेय है, जिस कारण से तुरंत यह बात आती है कि π भी अपरिमेय है। अबीजीय संख्या का अस्तित्व सर्वप्रथम लिओविले द्वारा स्थापित किया गया था (1844, 1851). बाद में, जोर्ज कैंटर (1873) ने एक भिन्न तरीके से उनके अस्तित्व को साबित कर दिया, जिसमें दर्शाया गया कि वास्तविक में हर अंतराल में अबीजीय संख्या शामिल होती है। चार्ल्स हर्मिट (1873) ने सबसे पहले e अबीजीय को साबित किया और फर्डिनेंड वॉन लिंडेमन (1882) ने हर्मिट के निष्कर्ष से शुरू करते हुए, π के लिए यही दर्शाया. लिंडेमन का सबूत विअरस्ट्रास (1885) द्वारा काफी सरलीकृत किया गया, बाद में डेविड हिल्बर्ट (1893) द्वारा और अंत में एडॉल्फ हुर्वित्ज़ और पॉल अल्बर्ट गोर्डन द्वारा प्राथमिक बनाया गया।
प्रमाण स्वरूप उदाहरण[संपादित करें]
वर्ग मूल[संपादित करें]
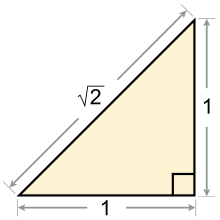
2 का वर्ग मूल वह पहली संख्या थी जिसे अपरिमेय साबित किया गया और उस लेख में कई सबूत शामिल हैं। सुनहरा अनुपात, अगला सबसे प्रसिद्ध द्विघात अपरिमेय है और उसके लेख में उसकी अपरिमेयता का एक सरल सबूत है। सभी गैर-वर्ग प्राकृतिक संख्या का वर्ग मूल, अपरिमेय है और द्विघात अपरिमेय में एक प्रमाण देखा जा सकता है।
2 के वर्गमूल की अपरिमेयता उसे परिमेय मानते हुए और एक विरोधाभास का निष्कर्ष निकालते हुए सिद्ध की जा सकती है, जिसे रिडक्शियो एड एब्सर्डम द्वारा एक तर्क कहा जाता है। निम्नलिखित तर्क इस तथ्य से दो बार अपील करता है कि एक विषम पूर्णांक का वर्ग हमेशा विषम होता है।
यदि √2 परिमेय है, तो पूर्णांक m,n के लिए इसका रूप m/n है, जहां दोनों सम नहीं हैं। फिर m 2 = 2n 2, इसलिए m सम है, कह लीजिये कि m = 2p . इस प्रकार 4p 2 = 2n 2 इसलिए 2p 2 = n 2 इसलिए n भी सम है, जो एक विरोधाभास है।
सामान्य वर्ग[संपादित करें]
दो के वर्गमूल के लिए उपर्युक्त सबूत को अंकगणित के मौलिक प्रमेय के उपयोग द्वारा सामान्यीकृत किया जा सकता है, जिसे 1798 में गॉस द्वारा साबित किया गया था। इससे यह बल मिलता है कि हर पूर्णांक का अभाज्य में अद्वितीय गुणनखंडन होता है। इसका इस्तेमाल करते हुए हम यह दिखा सकते हैं कि यदि एक परिमेय संख्या एक पूर्णांक नहीं है तो उसका कोई अभिन्न घात एक पूर्णांक नहीं हो सकता है, क्योंकि अपने न्यूनतम पद में हर में एक गुणनखंड होना चाहिए जो गणक से विभाजित नहीं होता चाहे दोनों ही किसी भी घात तक बढ़ा दिए जाएं. इसलिए अगर एक पूर्णांक, एक अन्य पूर्णांक का सटीक k वां घात नहीं है तो उसका k वां वर्ग अपरिमेय है।
लघुगणक[संपादित करें]
वे संख्याएं जिन्हें सबसे आसानी से अपरिमेय साबित किया जाता है वे शायद कुछ ख़ास लघुगणक है। यहां रिडक्शियो एड एब्सर्डम द्वारा एक सबूत है कि log2 3 अपरिमेय है। ध्यान दें कि log2 3 ≈ 1.58> 0.
मान लीजिये कि log2 3 परिमेय है। कुछ धनात्मक पूर्णांक m और n के लिए, हमारे पास है
इसका मतलब है कि
हालांकि, संख्या 2 जिसे किसी भी धनात्मक पूर्णांक घात में बढ़ाया गया हो उसे सम होना चाहिए (क्योंकि वह 2 से विभाज्य होगा) और संख्या 3 को जिसे किसी भी धनात्मक पूर्णांक घात में बढ़ाया गया हो उसे विषम होना चाहिए (क्योंकि उसका कोई भी अभाज्य गुणनखंड 2 नहीं होगा). जाहिर है, एक पूर्णांक एक ही समय में सम और विषम, दोनों नहीं हो सकता: हमारे पास एक विरोधाभास है। जो एकमात्र अनुमान हमने लगाया था वह था कि log2 3 परिमेय है (और इसलिए पूर्णांक m /n के एक भागफल के रूप में व्यक्त होने में सक्षम है जहां n ≠ 0 है). विरोधाभास का मतलब है कि यह धारणा ज़रूर गलत होगी, यानी log2 3 अपरिमेय है और इसे कभी भी पूर्णांक m /n के एक भागफल के रूप में व्यक्त नहीं किया जा सकता है जहां n ≠ 0 है।
log10 2 जैसे मामलों के साथ भी इसी तरह का व्यवहार किया जा सकता है।
अबीजीय और बीजीय अपरिमेय[संपादित करें]
लगभग सभी अपरिमेय संख्याएं अबीजीय हैं और सभी अबीजीय संख्याएं अपरिमेय हैं: अबीजीय संख्या वाला लेख कई उदाहरणों को सूचीबद्ध करता है। e r और πr अपरिमेय हैं अगर r ≠ 0 परिमेय है; e π अपरिमेय है।
अपरिमेय संख्या को निर्मित करने का दूसरा तरीका है अपरिमेय बीजीय संख्या के रूप में निर्माण, यानी पूर्णांक गुणांक के साथ बहुपद के शून्य के रूप में: बहुपद समीकरण के साथ शुरू कीजिये
जहां गुणांक a i पूर्णांक हैं। मान लीजिए आप जानते हैं कि कुछ वास्तविक संख्याएं x मौजूद हैं जहां p (x) = 0 (उदाहरण के लिए यदि n विषम है और a n गैर-शून्य है, तब मध्यवर्ती प्रमेय मान की वजह से). इस बहुपद समीकरण का एकमात्र संभावित परिमेय मूल r /s स्वरूप में होगा जहां r, a 0 का एक भाजक है और s, a n का एक भाजक है; ऐसे केवल सीमित उम्मीदवार हैं जिसे आप सिर्फ हाथों से जांच सकते हैं। अगर उनमें से कोई भी p का मूल नहीं है, तो x ज़रूर अपरिमेय होना चाहिए। उदाहरण के लिए, इस तकनीक का इस्तेमाल यह दिखाने के लिए किया जा सकता है कि x = (21/2 + 1)1/3 अपरिमेय है: हमारे पास है (x 3 - 1)2 = 2 और इसलिए x 6 - 2x 3 - 1 = 0 और इस बाद वाले बहुपद में कोई परिमेय मूल नहीं है (जांच करने के लिए एकमात्र उम्मीदवार हैं ± 1).
क्योंकि बीजीय संख्या एक क्षेत्र गठित करते हैं, कई अपरिमेय संख्याओं को बीजीय और अबीजीय संख्याओं के संयोजन द्वारा निर्मित किया जा सकता है। उदाहरण के लिए 3π + 2, π + √2 और e √3 अपरिमेय हैं (और यहां तक कि अबीजीय).
दशमलव विस्तार[संपादित करें]
एक अपरिमेय संख्या का दशमलव विस्तार, एक परिमेय संख्या के विपरीत कभी दोहराता या समाप्त नहीं होता।
यह दर्शाने के लिए, मान लीजिये हम n पूर्णांक को m द्वारा भाग देते हैं (जहां m गैर-शून्य है). जब m द्वारा n के भाग पर दीर्घ भाग को लागू किया जाता है, तो केवल m शेषफल संभव होते हैं। यदि 0 एक शेषफल के रूप में प्रकट होता है, तो दशमलव विस्तार समाप्त हो जाता है। यदि 0 कभी प्रकट नहीं होता तो वह एल्गोरिथ्म, किसी भी शेषफल को एक बार से अधिक उपयोग ना करते हुए अधिक से अधिक m - 1 चरण चल सकता है। उसके बाद, एक शेषफल की पुनरावृत्ति होनी ही चाहिए और तब दशमलव विस्तार दोहराता है।
इसके विपरीत, मान लीजिये हमारे सामने एक आवर्ती दशमलव आता है, तो हम सिद्ध कर सकते हैं कि वह दो पूर्णांकों का भिन्न है। उदाहरण के लिए:
यहां रेपिटेंड की लंबाई 3 है। हम 103 से गुणा करते हैं:
ध्यान दें कि जब हमने 10 के घाते दोहराए जाने वाले भाग की लंबाई से गुणा किया, तो हमने अंकों को दशमलव बिंदु के बाईं ओर ठीक उतने ही स्थानों से स्थानांतरित किया। इसलिए, 1000A का पिछला सिरा बिल्कुल A के पिछले सिरे से मेल खाता है। यहां, दोनों 1000A और A के सिरे में 162 दोहराव है।
इसलिए, जब हम दोनों पक्षों से A को घटाते हैं, तो 1000A का पिछला सिरा A के पिछले सिरे से बाहर रद्द हो जाता है:
फिर
(7155 और 9990 का महत्तम आम भाजक है 135). वैकल्पिक रूप से, चूंकि 0.5 = 1/2 है, एक व्यक्ति अंश और हर को 2 से गुणा करके भिन्न को साफ़ कर सकता है:
(1431 और 1998 का महत्तम आम भाजक है 27).
अंतिम पंक्ति, 53/74, पूर्णांकों का एक भागफल है और इसलिए एक परिमेय संख्या है।
विविध[संपादित करें]
यहां एक प्रसिद्ध शुद्ध अस्तित्व या गैर-रचनात्मक प्रमाण है:
वहां दो अपरिमेय संख्याएं a और b मौजूद हैं, इस प्रकार कि a b परिमेय है। वास्तव में, अगर √2√2 परिमेय है, तब मानिये कि a = b = √2. अन्यथा, मान लीजिये कि a अपरिमेय संख्या √2√2 है और b = √2. तो फिर a b = (√2√2)√2 = 2√2·√2 = √22 = 2 जो परिमेय है।
हालांकि उपर्युक्त दलील दोनों मामलों के बीच निर्णय नहीं करती, गेल्फोंड-श्नाईडर प्रमेय का तात्पर्य है कि √2√2 अबीजीय है, इसलिए अपरिमेय है।
मुक्त प्रश्न[संपादित करें]
यह ज्ञात नहीं है कि क्या π + e अथवा π - e अपरिमेय है या नहीं। वास्तव में, वहां गैर-शून्य पूर्णांक m और n का कोई युग्म नहीं है जिसके बारे में यह ज्ञात हो कि क्या m π + ne अपरिमेय है या नहीं। इसके अलावा, यह ज्ञात नहीं है कि सेट (π, e) Q पर बीजगणित के अनुसार स्वतंत्र है या नहीं।
यह ज्ञात नहीं है कि क्या 2e , πe , π√2, कातालान निरंतर, या युलर-मेश्चेरोनी गामा निरंतर γ अपरिमेय हैं या नहीं।
सभी अपरिमेय का सेट[संपादित करें]
चूंकि वास्तविक एक अगणनीय सेट का गठन करते हैं, जिनमें से परिमेय एक गणनीय सबसेट होते हैं, अपरिमेय का पूरक सेट अगणनीय है।
सामान्य (इयूक्लिडियन) सुदूर क्रिया d (x, y) = |x - y |, वास्तविक संख्या एक मीट्रिक स्पेस है और इसलिए एक सांस्थितिकीय स्पेस भी है। इयूक्लिडियन सुदूर क्रिया को सीमित करने से अपरिमेय को एक मीट्रिक स्पेस की संरचना मिलती है। चूंकि अपरिमेय का उपस्पेस बंद नहीं है, उत्प्रेरित मीट्रिक पूर्ण नहीं है। हालांकि, एक पूर्ण मीट्रिक स्थान में G-डेल्टा सेट होते हुए - अर्थात् खुले सबसेट का एक गणनीय प्रतिच्छेदन - अपरिमेय का स्थान सांस्थितिकी रूप से पूर्ण है: अर्थात्, अपरिमेय पर एक मीट्रिक है जो ठीक वैसी ही सांस्थितिकी को उत्प्रेरित करता है जैसा कि इयूक्लिडियन मीट्रिक का प्रतिबंध करता है, लेकिन जिसके संबंध में अपरिमेय पूर्ण हैं। एक व्यक्ति G-डेल्टा सेट के बारे में ऊपर उल्लिखित तथ्य से अनभिज्ञ रहते भी इसे देख सकता है: एक अपरिमेय संख्या का सतत भिन्न विस्तार, अपरिमेय के स्थान से सभी धनात्मक पूर्णांक के स्थान तक एक होमिओमोर्फिज़म को परिभाषित करता है, जिसे आसानी से पूर्ण रूप से मेट्रिक योग्य देखा जाता है।
इसके अलावा, सभी अपरिमेय के सेट, कटे हुए एक मेट्रिक-योग्य स्थान हैं। वास्तव में, अपरिमेय में क्लोपेन सेट का आधार होता है इसलिए स्थान शून्य-आयामी होता है।
== इन्हें भी देखें ==√8
- जो एक अपरिमेय संख्या है,
- e भी एक अपरिमेय संख्या है
- २ का वर्गमूल
- 3 का वर्गमूल
- n वां मूल
सन्दर्भ[संपादित करें]
- ↑ साँचा:Harvrefcol. ISBN 978-0-486-60045-1
- ↑ The 15 Most Famous Transcendental Numbers Archived 2007-10-24 at the वेबैक मशीन. क्लिफर्ड ए. पिकोवर द्वारा URL 24 अक्टूबर 2007 को पुनः प्राप्त.
- ↑ ; http://www.mathsisfun.com/irrational-numbers.html Archived 2010-08-29 at the वेबैक मशीन URL पुनः प्राप्त 24 अक्टूबर 2007.
- ↑ एरिक डब्ल्यू वेइसटीन, मैथवर्ल्ड पर Irrational Number यूआरएल पुनः प्राप्त 26 अक्टूबर 2007.
- ↑ टीके पुट्टास्वामी, "प्राचीन भारतीय गणितज्ञों की उपलब्धियां", pp. 411-2 Selin, Helaine; D'Ambrosio, Ubiratan (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. आई॰ऍस॰बी॰ऍन॰ 1402002602. .
- ↑ Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics.
- ↑ James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal.
- ↑ क्लाइन, एम. (1990). मेथेमेटिकल थोट्स फ्रॉम एन्शिएन्ट टु मॉडर्न टाइम्स. 1. न्यूयॉर्क: ऑक्सफोर्ड विश्वविद्यालय प्रेस. (मूल कृति 1972 में प्रकाशित). p.33.
- ↑ क्लाइन 1990, p. 32.
- ↑ Robert L. McCabe (1976). "Theodorus' Irrationality Proofs". Mathematics Magazine. .
- ↑ Charles H. Edwards (1982). The historical development of the calculus. Springer.
- ↑ क्लाइन 1990, p.48.
- ↑ क्लाइन 1990, p.49.
- ↑ ओ'कॉनर, जॉन; रॉबर्टसन, एडमण्ड, "Arabic mathematics: forgotten brilliance?", मैक्ट्यूटर हिस्ट्री ऑफ़ मैथेमैटिक्स, युनिवर्सिटी ऑफ़ सैंट एण्ड्रूज़. .
- ↑ Matvievskaya, Galina (1987). "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics". Annals of the New York Academy of Sciences. 500: 253–277 [254]. डीओआइ:10.1111/j.1749-6632.1987.tb37206.x. .
- ↑ अ आ Matvievskaya, Galina (1987). "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics". Annals of the New York Academy of Sciences. 500: 253–277 [259]. डीओआइ:10.1111/j.1749-6632.1987.tb37206.x.
- ↑ जैक्स सेसिअनो, "इस्लामिक मैथेमेटिक्स", p. 148 Selin, Helaine; D'Ambrosio, Ubiratan (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. आई॰ऍस॰बी॰ऍन॰ 1402002602. में.
- ↑ Matvievskaya, Galina (1987). "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics". Annals of the New York Academy of Sciences. 500: 253–277 [260]. डीओआइ:10.1111/j.1749-6632.1987.tb37206.x. .
- ↑ Matvievskaya, Galina (1987). "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics". Annals of the New York Academy of Sciences. 500: 253–277 [261]. डीओआइ:10.1111/j.1749-6632.1987.tb37206.x. .
- ↑ कैट्ज़, वीजे (1995), "इस्लाम और भारत में कलन का विचार", मैथेमेटिक्स मैग्ज़ीन (मेथेमेटिकल एसोसिएशन ऑफ़ अमेरिका) 68 (3): 163-74.
- ↑ Salvatore Pincherle (1880). "Saggio di una introduzione alla teorica delle funzioni analitiche secondo i principi del prof. Weierstrass". Giornale di Matematiche.
- ↑ J. H. Lambert (1761). "Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques". Histoire de l'Académie Royale des Sciences et des Belles-Lettres der Berlin: 265–276.
अतिरिक्त पठन[संपादित करें]
- एड्रियन-मारी लेगेंद्र, Éléments de Géometrie, नोट IV, (1802), पेरिस
- रॉल्फ वालिसर, अल्जेब्रिक नंबर थिओरी एंड डायोफेंटाइन अनैलिसिस में "ऑन लेम्बर्ट्स प्रूफ ऑफ़ द इर्रेशनैलिटी ऑफ़ π", फ्रांज हाल्टर-कॉख और रॉबर्ट एफ टीचि, (2000), वाल्टर डे ग्रुयर
बाहरी कड़ियाँ[संपादित करें]



















