पेजरैंक

सरल नेटवर्क (गूगल द्वारा पेजरैंक्स की सूचना लघुगणकीय रिस्केल्ड हैं) के लिए गणितीय पेजरैंक्स (100 में से).पृष्ठ E से पेज C के पेजरैंक ज्यादा है, भले ही उसके लिंक कम हैं; परन्तु जो लिंक है वे बहुत अधिक मान के हैं। एक वेब सर्फर जो प्रत्येक पृष्ठ (उन पर 15% संभावना के साथ पूरे वेब पर एक यादृच्छिक पृष्ठ पर छलांग) पर यादृच्छिक लिंक का चयन करता है, वह समय का 8.1% पृष्ठ E पर रहने जा रहा है। एक पृष्ठ पर यादृच्छिक रूप से छलांग लगाने की 15%संभावना अवमन्दन कारक के 85% से संबंधित है। बिना अवमन्दन के, सारे वेब सर्फर्स पृष्ठ A, B या C पर ख़त्म करेंगे और बाकी के सारे पृष्ठों के पेजरैंक जीरो होंगे.पृष्ठ A को वेब के सभी पृष्ठों से जुड़ा माना जाता है, क्योंकि इसका कोई निर्गामी लिंक नहीं है।

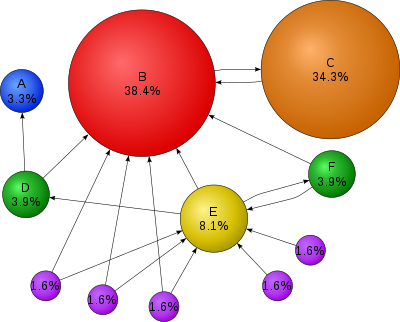
पेजरैंक, जिसका नाम लैरी पेज के नाम पर रखा गया है, गूगल सर्च इंजन द्वारा प्रयोग किया जाने वाला एक लिंक विश्लेषण अल्गोरिथम है, जो दस्तावेजों के एक हाइपरलिंक-बद्ध समुच्चय, जैसे वर्ल्ड वाइड वेब, के प्रत्येक तत्व को एक अंकीय भार आवंटित करता है, ताकि समुच्चय के भीतर उसके सापेक्ष महत्व का "मापन" किया जा सके। यह अल्गोरिथम पारस्परिक उद्धरणों और संदर्भों के साथ तत्वों के किसी भी संग्रह पर लागू किया जा सकता है। दिये गये किसी तत्व E को आवंटित किये जाने वाले संख्यात्मक भार को E का पेजरैंक कहते हैं और इसे $PR(E).$ द्वारा दर्शाया जाता है।

"पेजरैंक" नाम गूगल का ट्रेडमार्क है और पेजरैंक प्रक्रिया का पेटेंट करवाया जा चुका है।अमेरिकी पेटेंट 62,85,999 हालांकि पेटेंट स्टैनफ़ोर्ड विश्वविद्यालय को दिया गया है, न कि गूगल को। गूगल के पास स्टैनफ़ोर्ड विश्वविद्यालय से प्राप्त विशिष्ट लाइसेंस अधिकार है। पेटेंट के प्रयोग के बदले विश्वविद्यालय को गूगल के 1.8 मिलियन शेयर मिले; ये शेयर 2005 में $336 मिलियन में बेच दिये गये।

वर्णन

गूगल पेजरैंक का वर्णन इस प्रकार करता है:

“

PageRank relies on the uniquely democratic nature of the web by using its vast link structure as an indicator of an individual page's value. In essence, Google interprets a link from page A to page B as a vote, by page A, for page B. But, Google looks at more than the sheer volume of votes, or links a page receives; it also analyzes the page that casts the vote. Votes cast by pages that are themselves "important" weigh more heavily and help to make other pages "important".

”

दूसरे शब्दों में, एक पेजरैंक वर्ल्ड वाइड वेब पर अन्य सभी पृष्ठों के बीच इस बारे में एक "मतदान" के द्वारा प्राप्त होता है कि कोई पृष्ठ कितना महत्वपूर्ण है। किसी पृष्ठ की ओर आने वाली एक हाइपरलिंक को समर्थन का एक मत माना जाता है। पृष्ठ का पेजरैंक दोहरावपूर्ण रूप से परिभाषित किया जाता है और यह उससे जुड़नेवाले सभी पृष्ठों ("आनेवाले लिंक") के पेजरैंक मेट्रिक और संख्या पर निर्भर होता है। जिस पृष्ठ के साथ उच्च पेजरैंक वाले अनेक पृष्ठों ने लिंक बनाए हों, उसे स्वतः ही एक उच्च रैंक मिलता है। यदि एक वेब पेज के लिये कोई लिंक न हों, तो उसके लिये कोई समर्थन नहीं होता।

गूगल इंटरनेट के प्रत्येक वेबपेज को 0-10 के बीच एक अंकीय भारण प्रदान करता है; यह पेजरैंक गूगल की नज़रों में किसी साइट के महत्व को सूचित करता है। पेजरैंक को प्राप्त करने के लिये रिक्टर पैमाने जैसे एक लघुगणकीय पैमाने पर एक सैद्धांतिक प्रायिकता का प्रयोग किया जाता है। किसी विशिष्ठ पृष्ठ का पेजरैंक मोटे तौर पर अंतर्गामी लिंक्स की मात्रा और साथ ही ये लिंक प्रदान करनेवाले पृष्ठों के पेजरैंक पर निर्भर होता है। यह ज्ञात है कि अन्य कारक, उदा. पृष्ठ पर खोज-शब्दों की उपयुक्तता और पृष्ठ पर वास्तविक भ्रमण की गूगल टूलबार द्वारा बताई गई संख्या भी पेजरैंक को प्रभावित करती है। हेराफ़ेरी, धोखेबाज़ी और स्पैमडेक्सिंग से बचाव के लिये, गूगल इस बारे में कोई विशिष्ट विवरण प्रदान नहीं करता कि अन्य कारक पेजरैंक को किस प्रकार प्रभावित करते हैं।

पेज और ब्रिन के मूल शोध-पत्र के बाद से पेजरैंक से संबंधित अनेक शैक्षणिक शोध-पत्र प्रकाशित हो चुके हैं। व्यवहार में, पेजरैंक की अवधारणा हेराफ़ेरी के प्रति असुरक्षित साबित हुई है और गलत तरीके से बढ़ाई गई पेजरैंक की पहचान और गलत तरीके से बढ़ाई गई पेजरैंक के साथ जुड़नेवाले दस्तावेजों को उपेक्षित करने के तरीकों के प्रति गहन अनुसंधान समर्पित है।

वेब पृष्ठों के लिये लिंक-आधारित अन्य एल्गोरिथमों में जॉन क्लीनबर्ग द्वारा खोजा गया HITS ऐल्गरिदम (Teoma और अब Ask.com द्वारा प्रयुक्त), IBM CLEVER परियोजना और TrustRank ऐल्गरिदम शामिल हैं।

इतिहास

पेजरैंक का विकास स्टैनफ़ोर्ड विश्वविद्यालय में लैरी पेज द्वारा (इसीलिए इसे पेज -रैंक नाम दिया गया) और बाद में सर्गेई ब्रिन द्वारा एक नए प्रकार के सर्च इंजन से संबंधित अनुसंधान परियोजना के एक भाग के रूप में किया गया। इस परियोजना के बारे में पहला शोध-पत्र, जिसमें पेजरैंक और Google search इंजन का प्रारंभिक प्रोटोटाइप था, 1998 में प्रकाशित हुआ: कुछ ही समय बाद पेज और ब्रिन ने Google Inc., गूगल सर्च इंजन की निर्माता कम्पनी, की स्थापना की। गूगल सर्च परिणामों की रैंकिंग को निर्धारित करनेवाले अनेक कारकों में से एक होने के साथ ही पेजरैंक गूगल के सभी वेब सर्च उपकरणों के लिये आधार भी प्रदान करता है।

पेजरैंक पर अवतरण विश्लेषण (citation analysis), पहले पेन्सिलवेनिया विश्वविद्यालय में 1950 के दशक में यूजीन गारफ़ील्ड द्वारा विकसित और हाइपर सर्च (Hyper Search), पैडुआ विश्वविद्यालय में मैसिमो मार्चिओरी द्वारा विकसित, से प्रभावित रहा है (गूगल के संस्थापकों ने अपने मूल शोध-पत्र में गारफ़ील्ड और मार्चिओरी के कार्यों को उद्धृत किया है). जिस वर्ष पेजरैंक को प्रस्तुत किया गया (1998), उसी वर्ष जॉन क्लीनबर्ग ने HITS पर अपना महत्वपूर्ण कार्य प्रकाशित किया।

2010 में, हार्वर्ड के एक अर्थशास्त्री और 1973 के नोबेल पुरस्कार विजेता वैसिली लिओंटीफ़ के 1941 के एक शोध-पत्र को पेजरैंक की दोहरावपूर्ण कार्यविधि के प्रारंभिक बौद्धिक पूर्ववर्ती के रूप में पहचाना गया।

अल्गोरिथम

पेजरैंक एक प्रायिकता वितरण है, जिसका प्रयोग यादृच्छिक रूप से लिंक्स पर क्लिक करनेवाले व्यक्ति के किसी विशिष्ट पृष्ठ पर पहुंचने की संभावना को प्रदर्शित करने के लिये किया जाता है। पेजरैंक की गणना किसी भी आकार के दस्तावेजों के संग्रह के लिये की जा सकती है। अनेक शोध पत्रों में यह माना जाता है कि गणना प्रक्रिया के प्रारंभ में ही यह वितरण संग्रह के सभी दस्तावेजों के बीच समान रूप से विभाजित कर दिया जाता है। पेजरैंक गणनाओं के लिये संग्रह के अनेक चक्रों को दोहराने की आवश्यकता होती है, जिन्हें "इटरेशन" कहते हैं, ताकि सैद्धांतिक रूप से शुद्ध मान को अधिक निकटता से प्रतिबिंबित करने हेतु पेजरैंक के अनुमानित मानों को समायोजित किया जा सके।

एक प्रायिकता 0 और 1 के बीच किसी संख्यात्मक मान के रूप में व्यक्त की जाती है। एक 0.5 प्रायिकता को सामान्यतः किसी कार्य के होने की "50% संभावना" के रूप में व्यक्त किया जाता है। अतः 0.5 पेजरैंक का अर्थ है कि इस बात की 50% संभावना है कि किसी यादृच्छिक लिंक पर क्लिक करनेवाला कोई व्यक्ति 0.5 पेजरैंक वाले किसी दस्तावेज की ओर भेजा जाएगा.

सरलीकृत अल्गोरिथम

पेजरैंक्स कैसे काम करते हैं।

चार वेब पृष्ठों: A, B, C और D, के एक छोटे से ब्रह्मांड पर विचार करें। पेजरैंक का प्रारंभिक अनुमान इन चारों दस्तावेजों के बीच समान रूप से बांटा जाएगा. अतः प्रत्येक दस्तावेज एक 0.25 के अनुमानित पेजरैंक के साथ प्रारंभ करेगा।

पेजरैंक के मूल रूप में प्रारंभिक मान केवल 1 होते थे। इसका अर्थ यह है कि सभी पृष्ठों का योगफल वेब पर पृष्ठों की कुल संख्या के बराबर था। पेजरैंक के बाद वाले संस्करण (नीचे दिये गये सूत्रों को देखें) 0 और 1 के बीच का प्रायिकता विभाजन मानते है। यहां एक सरल प्रायिकता वितरण का प्रयोग किया जाएगा- अतः प्रारंभिक मान 0.25 लिया गया है।

यदि पृष्ठ B, C और D केवल A के लिये लिंक प्रदान करते हैं, तो उनमें से प्रत्येक पृष्ठ A को 0.25 पेजरैंक प्रदान करेगा। इस प्रकार इस सरल प्रणाली में सभी पेजरैंक PR() A पर एकत्रित हों जाएंगे क्योंकि सभी लिंक्स A को सूचित कर रहे होंगे।

$PR(A)=PR(B)+PR(C)+PR(D).\,$

यह 0.75 है।

पुनः, माना कि पृष्ठ B के पास पृष्ठ C के लिये भी एक लिंक है और पृष्ठ D के पास तीनों पृष्ठों के लिये लिंक है। लिंक-मतों का मान किसी पृष्ठ पर स्थित सभी बहिर्गामी लिंक्स के बीच विभाजित किया जाता है। इस प्रकार पृष्ठ B द्वारा पृष्ठ A को दिये जाने वाले मत का मूल्य 0.125 और पृष्ठ C को दिये जाने वाले मत का मूल्य 0.125 है। D के पेजरैंक के केवल एक-तिहाई भाग की गणना ही A के पेजरैंक के लिये की जाती है (लगभग 0.083).

$PR(A)={\frac {PR(B)}{2}}+{\frac {PR(C)}{1}}+{\frac {PR(D)}{3}}.\,$

दूसरे शब्दों में, बहिर्गामी पृष्ठों द्वारा प्रदान किया जाने वाला पेजरैंक दस्तावेज के स्वयं के पेजरैंक स्कोर और बहिर्गामी लिंक्स की प्रसामान्यीकृत (normalized) संख्या L() के भागफल के बराबर होता है (ऐसा माना जाता है कि विशिष्ट URLs की ओर जाने वाले लिंक्स को प्रत्येक दस्तावेज में केवल एक बार गिना गया है).

$PR(A)={\frac {PR(B)}{L(B)}}+{\frac {PR(C)}{L(C)}}+{\frac {PR(D)}{L(D)}}.\,$

सामान्य स्थिति में, किसी पृष्ठ u के पेजरैंक मान को इस प्रकार व्यक्त किया जा सकता है:

$PR(u)=\sum _{v\in B_{u}}{\frac {PR(v)}{L(v)}}$

अर्थात पृष्ठ u का पेजरैंक मान समुच्च्य B_u (इस समुच्च्य में पृष्ठ u से लिंक होने वाले सभी पृष्ठ होते हैं) के प्रत्येक पृष्ठ v के पेजरैंक मान और पृष्ठ v से निकलनेवाले लिंक्स की संख्या L (v) के भागफल पर निर्भर होता है।

उदासीनता कारक

पेजरैंक सिद्धांत मानता है कि लिंक्स पर यादृच्छिक रूप से क्लिक करनेवाला कोई काल्पनिक प्रयोक्ता भी अंततः क्लिक करना बंद कर देगा। किसी भी चरण में, व्यक्ति द्वारा कार्य जारी रखे जाने की संभावना, एक उदासीनता कारक d होती है। विभिन्न अध्ययनों ने विभिन्न उदासीनता कारकों का परीक्षण किया है, लेकिन सामान्यतः यह माना जाता है कि उदासीनता कारक 0.85 के आस-पास निर्धारित किया जाएगा.

उदासीनता कारक को 1 से घटाया जाता है (और ऐल्गरिदम के कुछ संस्करणों में, परिणाम को संग्रह में दस्तावेजों की संख्या (N) से भाग दिया जाता है) और इसके बाद इस मान को उदासीनता कारक और अंतर्गामी पेजरैंक स्कोर से गुणनफल में जोड़ा जाता है। अर्थात,

$PR(A)={1-d \over N}+d\left({\frac {PR(B)}{L(B)}}+{\frac {PR(C)}{L(C)}}+{\frac {PR(D)}{L(D)}}+\,\cdots \right).$

अतः किसी भी पृष्ठ का पेजरैंक मुख्यतः अन्य पृष्ठों के पेजरैंक से प्राप्त किया जाता है। प्राप्त किये गये मान को उदासीनता कारक नीचे की ओर समायोजित करता है। हालांकि मूल शोध-पत्र में एक भिन्न सूत्र दिया गया, जिससे कुछ भ्रम की स्थिति उत्पन्न हुई:

$PR(A)=1-d+d\left({\frac {PR(B)}{L(B)}}+{\frac {PR(C)}{L(C)}}+{\frac {PR(D)}{L(D)}}+\,\cdots \right)$

इन दोनों के बीच अंतर यह है कि पहले सूत्र में पेजरैंक मानों का योगफल एक होता है, जबकि दूसरे सूत्र में प्रत्येक पेजरैंक का N से गुणा किया जाता है और योगफल N बन जाता है। पेज और ब्रिन के शोध-पत्र का एक कथन कि "सभी पेजरैंकों का योगफल एक होता है" और गूगल के अन्य कर्मचारियों के दावे उपरोक्त सूत्र के पहले संस्करण का समर्थन करते हैं।

प्रत्येक बार वेब को क्रॉल करने पर गूगल पेजरैंक के स्कोर की पुनर्गणना करता है और अपने सूचकांक का पुनर्निर्माण करता है। गूगल द्वारा अपने संग्रहण में दस्तावेजों की संख्या बढ़ाये जाने के साथ ही, सभी दस्तावेजों के लिये पेजरैंक का प्रारंभिक अनुमान भी घटता जाता है।

यह सूत्र रैंडम सर्फ़र के एक मॉडल का प्रयोग करता है, जो कुछ क्लिक के बाद ऊब जाता है और किसी यादृच्छिक पृष्ठ की ओर चला जाता है। किसी पृष्ठ का पेजरैंक मान इस बात की संभावना को प्रतिबिंबित करता है कि रैंडम सर्फ़र किसी लिंक पर क्लिक करके उस पृष्ठ पर पहुंचेगा. इसे एक मार्कोव श्रृंखला के रूप में समझा जा सकता है, जिसमें अवस्थाएं पृष्ठ होती हैं और सभी परिवर्तनों की प्रायिकता समान होती है और वे पृष्ठों के बीच लिंक होते हैं।

यदि किसी पृष्ठ पर अन्य पृष्ठों के लिये कोई लिंक न हों, तो वह एक सिंक बन जाता है और इस कारण वह यादृच्छिक सर्फिंग प्रक्रिया को समाप्त कर देता है। हालांकि, समाधान बहुत सरल है। यदि यादृच्छिक सर्फर एक सिंक पृष्ठ पर आता है, तो वह यादृच्छिक रूप से कोई अन्य URL चुनता है और पुनः सर्फिंग जारी रखता है।

जिन पृष्ठों में कोई बहिर्गामी लिंक न हों, पेजरैंक की गणना करते समय उन्हें संग्रह के अन्य सभी पृष्ठों से जुड़ा हुआ माना जाता है। अतः उनके पेजरैंक स्कोर अन्य सभी पृष्ठों के बीच बराबर बंट जाते हैं। दूसरे शब्दों में, जो पृष्ठ सिंक नहीं हैं, उनके साथ न्याय करने के लिये, ये यादृच्छिक परिवर्तन वेब में सभी नोड्स में, सामान्यतः d =0.85 की एक शेष प्रायिकता के साथ जोड़े जाते हैं, जिसका आकलन इस आवृत्ति से किया जाता है कि एक औसत सर्फर अपने ब्राउज़र की बुकमार्क विशेषता का प्रयोग करता है।

अतः समीकरण इस प्रकार होता है:

$PR(p_{i})={\frac {1-d}{N}}+d\sum _{p_{j}\in M(p_{i})}{\frac {PR(p_{j})}{L(p_{j})}}$

जहां $p_{1},p_{2},...,p_{N}$ वे पृष्ठ हैं, जिन पर विचार किया जा रहा है, $M(p_{i})$ उन पृष्ठों का समुच्चय है, जो $p_{i}$ से जुड़ते हैं, $L(p_{j})$ पृष्ठ $p_{j}$ पर बहिर्गामी लिंक्स की संख्या है और N पृष्ठों की कुल संख्या है।

पेजरैंक मान संशोधित निकटता मैट्रिक्स के प्रभावी आइजन्वेक्टर की प्रविष्टियां होती हैं। यह पेजरैंक को एक विशिष्ट रूप से आकर्षक मेट्रिक्स बनाता है: आइजन्वेक्टर है

$\mathbf {R} ={\begin{bmatrix}PR(p_{1})\\PR(p_{2})\\\vdots \\PR(p_{N})\end{bmatrix}}$

जहां R समीकरण का हल है

$\mathbf {R} ={\begin{bmatrix}{(1-d)/N}\\{(1-d)/N}\\\vdots \\{(1-d)/N}\end{bmatrix}}+d{\begin{bmatrix}\ell (p_{1},p_{1})&\ell (p_{1},p_{2})&\cdots &\ell (p_{1},p_{N})\\\ell (p_{2},p_{1})&\ddots &&\vdots \\\vdots &&\ell (p_{i},p_{j})&\\\ell (p_{N},p_{1})&\cdots &&\ell (p_{N},p_{N})\end{bmatrix}}\mathbf {R}$

जहां निकटता फंक्शन $\ell (p_{i},p_{j})$ 0 होता है, यदि पृष्ठ $p_{i}$ पृष्ठ $p_{j}$ से न जुड़ता हो और इसका प्रसामान्यीकरण इस प्रकार किया जाता है कि प्रत्येक i के लिये

$\sum _{i=1}^{N}\ell (p_{i},p_{j})=1$

अर्थात, प्रत्येक स्तंभ के तत्वों का योगफल 1 तक होता है (अधिक जानकारी के लिये नीचे गणना खण्ड देखें). यह आइजन्वेक्टर केंद्रीयता मापन का एक संस्करण है, जिसका प्रयोग सामान्यतः नेटवर्क विश्लेषण में किया जाता है।

उपरोक्त संशोधित आइजनवेक्टर मेट्रिक्स में बड़े आइजनगैप के कारण पेजरैंक आइजन्वेक्टर के मानों का अनुमान तीव्रता से लगाया जा सकता है (केवल कुछ ही दोहरावों की आवश्यकता होती है).

मार्कोव सिद्धांत के फलस्वरूप, यह दर्शाया जा सकता है कि किसी पृष्ठ का पेजरैंक अनेक क्लिक के बाद उस पृष्ठ पर होने की प्रायिकता होता है। यह $t^{-1}$ के बराबर होता है, जहां $t$ किसी पृष्ठ से पुनः उसी पृष्ठ पर वापस आने के लिये आवश्यक क्लिक (या यादृच्छिक छलांग) की संख्या का अनुमान है।

इसकी मुख्य कमी यह है कि यह पुराने पृष्ठों के प्रति पक्षपात करता है क्योंकि नया पृष्ठ, चाहे वह बहुत अच्छा भी हो, जब तक किसी पुरानी साइट का एक भाग न हो, तब तक उसके पास अनेक लिंक्स नहीं होंगे (क्योंकि साइट पृष्ठों का एक गहन रूप से जुड़ा हुआ समूह होती है, जैसे विकिपीडिया). गूगल डायरेक्ट्री (जो कि स्वयं ओपन डायरेक्ट्री प्रोजेक्ट से व्युत्पन्न है) प्रयोक्ताओं को श्रेणियों के अंतर्गत पेजरैंक के अनुसार क्रमबद्ध किये गए पृष्ठों को देखने की अनुमति देती है। गूगल डायरेक्ट्री गूगल द्वारा प्रदान की जाने वाली एकमात्र सेवा है, जहां पेजरैंक निर्देशिका प्रदर्शन क्रम का निर्धारण करती है।^{[उद्धरण चाहिए]} गूगल की अन्य खोज सेवाओं (जैसे इसकी प्राथमिक वेब खोज) में पेजरैंक का प्रयोग खोज के परिणामों में प्रदर्शित पृष्ठों के प्रासंगिक स्कोर के मापन के लिये किया जाता है।

पेजरैंक की गणना को गति प्रदान करने के लिये विभिन्न रणनीतियां प्रस्तावित की गईं हैं।

खोज के परिणामों की रैंकिंग में सुधार करने और विज्ञापन लिंक्स का मुद्रीकरण करने के मज़बूत प्रयासों के अंतर्गत पेजरैंक में परिवर्तन करने के लिये विभिन्न रणनीतियां लागू की गईं हैं। इन रणनीतियों ने पेजरैंक की अवधारणा की विश्वसनीयता को अत्यधिक प्रभावित किया है, जो यह निर्धारित करने का प्रयास करती है कि वास्तव में किन दस्तावेजों को वेब समुदाय द्वारा उच्च मान दिया जाता है।

गूगल को लिंक फार्म और कृत्रिम रूप से पेजरैंक को बढ़ाने के लिये बनाई गई अन्य योजनाओं को दण्डित करने के लिये जाना जाता है। दिसम्बर 2007 में, गूगल ने भुगतान के द्वारा टेक्स्ट लिंक बेचने वाली साइटों को सक्रिय रूप से दण्डित करना शुरु किया। गूगल द्वारा लिंक फार्मों और पेजरैंक में परिवर्तन करने के अन्य उपकरणों की पहचान किस प्रकार की जाती है, यह गूगल के व्यापारिक रहस्यों में से एक है।

गणना

संक्षेप में, पेजरैंक की गणना दोहरावपूर्ण रूप से या बीजगणितीय रूप से की जा सकती है। वैकल्पिक तौर पर घात दोहराव विधि, या घात विधि, का प्रयोग किया जा सकता है।

दोहरावपूर्ण

पहली स्थिति में, $t=0$ पर, एक प्रारंभिक प्रायिकता वितरण माना जाता है, सामान्यतः

$PR(p_{i};0)={\frac {1}{N}}$

जैसा कि ऊपर वर्णित है, प्रत्येक समय चरण पर गणना निम्नलिखित परिणाम प्रदान करती है

$PR(p_{i};t+1)={\frac {1-d}{N}}+d\sum _{p_{j}\in M(p_{i})}{\frac {PR(p_{j};t)}{L(p_{j})}}$

या मैट्रिक्स संकेतन में

$\mathbf {R} (t+1)=d{\mathcal {M}}\mathbf {R} (t)+{\frac {1-d}{N}}\mathbf {1}$, (*)

जहां $\mathbf {R} _{i}(t)=PR(p_{i};t)$ और $\mathbf {1}$ केवल एक को रखनेवाला $N$ लंबाई का स्तंभ वेक्टर है।

मेट्रिक्स ${\mathcal {M}}$ को इस प्रकार परिभाषित किया जाता है

${\mathcal {M}}_{ij}={\begin{cases}1/L(p_{j}),&{\mbox{if }}j{\mbox{ links to }}i\ \\0,&{\mbox{otherwise}}\end{cases}}$

अर्थात,

${\mathcal {M}}:=(K^{-1}A)^{t}$

जहां $A$ ग्राफ के निकटता मेट्रिक्स को सूचित करता है और $K$ विकर्ण में बाहरी डिग्री के साथ एक विकर्ण मेट्रिक्स है।

गणना तब समाप्त होती है, जब किसी छोटे $\epsilon$ के लिये

$|\mathbf {R} (t+1)-\mathbf {R} (t)|$

अर्थात जब अभिसरण माना जाता है।

बीजगणितीय

दूसरी स्थिति में, $t\to \infty$ (अर्थात, स्थिर अवस्था में), उपरोक्त समीकरण (*) इस प्रकार होता है

$\mathbf {R} =d{\mathcal {M}}\mathbf {R} +{\frac {1-d}{N}}\mathbf {1}$       (**)

समाधान निम्नलिखित के द्वारा दिया जाता है

$\mathbf {R} =(\mathbf {I} -d{\mathcal {M}})^{-1}{\frac {1-d}{N}}\mathbf {1}$

पहचान मेट्रिक्स के $\mathbf {I}$ साथ.

समाधान उपलब्ध है और यह $0$ के लिये अद्वितीय होता है। इसे इस बात पर ध्यान देने पर देखा जा सकता है कि ${\mathcal {M}}$ अपने निर्माण के द्वारा एक स्टोकेस्टिक मेट्रिक्स है और इसलिये पेरोन-फ्रोबेनियस प्रमेय के कारण इसका आइजनमान एक है।

घात विधि

यदि मेट्रिक्स ${\mathcal {M}}$ एक परिवर्तन संभावना है, अर्थात स्तंभ-स्टोकेस्टिक, जिसमें किसी स्तंभ में केवल शून्य नहीं हैं और $\mathbf {R}$ एक प्रायिकता वितरण है (अर्थात, $|\mathbf {R} |=1$), समीकरण (**) निम्नलिखित के समतुल्य है

$\mathbf {R} =\left(d{\mathcal {M}}+{\frac {1-d}{N}}\mathbf {I} \right)\mathbf {R} =:{\widehat {\mathcal {M}}}\mathbf {R}$       (***)

इस प्रकार पेजरैंक $\mathbf {R}$, ${\widehat {\mathcal {M}}}$ का मुख्य आइजन्वेक्टर है। इसकी गणना करने की एक तेज़ और सरल पद्धति घात विधि का प्रयोग करना है: एक अनियंत्रित वेक्टर $x(0)$ से शुरु करते हुए, ऑपरेटर ${\widehat {\mathcal {M}}}$ को अनुक्रम में लागू किया जाता है, अर्थात,

$x(t+1)={\widehat {\mathcal {M}}}x(t)$

जब तक

$|x(t+1)-x(t)|$ न हो.

ध्यान दें कि समीकरण (***) में, दाहिनी ओर कोष्ठकों में लिखे मेट्रिक्स की व्याख्या इस प्रकार की जा सकती है

${\frac {1-d}{N}}\mathbf {I} =(1-d)\mathbf {P} \mathbf {1} ^{t}$

जहां $\mathbf {P}$ एक प्रारंभिक प्रायिकता वितरण है। वर्तमान स्थिति में

$\mathbf {P} :={\frac {1}{N}}\mathbf {1}$

अंततः, यदि ${\mathcal {M}}$ में केवल शून्य मान वाले स्तंभ हों, तो उनके स्थान पर प्रारंभिक संभावना वेक्टर $\mathbf {P}$ रखा जाना चाहिये। दूसरे शब्दों में

${\mathcal {M}}^{\prime }:={\mathcal {M}}+{\mathcal {D}}$

जहां मेट्रिक्स ${\mathcal {D}}$ को इस प्रकार परिभाषित किया जाता है।

${\mathcal {D}}:=\mathbf {D} \mathbf {P} ^{t}$

निम्नलिखित के साथ

$\mathbf {D} _{i}={\begin{cases}1,&{\mbox{if }}L(p_{i})=0\ \\0,&{\mbox{otherwise}}\end{cases}}$

केवल ${\mathcal {M}}$ का प्रयोग करनेवाली उपरोक्त दोनों गणनाएं समान पेजरैंक प्रदान करती हैं, यदि उनके परिणाम प्रसामान्यीकृत न हों.

$\mathbf {R} _{\textrm {power}}={\frac {\mathbf {R} _{\textrm {iterative}}}{|\mathbf {R} _{\textrm {iterative}}|}}={\frac {\mathbf {R} _{\textrm {algebraic}}}{|\mathbf {R} _{\textrm {algebraic}}|}}$

दक्षता

गणना के लिये प्रयुक्त ढ़ांचे, इन विधियों के सटीक क्रियान्वयन और परिणामों की आवश्यक अचूकता के आधार पर इन तीन विधियों के गणना समय में बहुत अधिक अंतर हो सकता है। सामान्यतः यदि गणना अनेक बार की जानी है (अर्थात बढ़ते हुए नेटवर्कों के लिये) अथवा नेटवर्क का आकार बड़ा है, तो मेट्रिक्स के उत्क्रमण के कारण बीजगणितीय गणना धीमी और अधिक मेमोरी लेने वाली होती है और घात विधि सर्वाधिक दक्ष होती है।

विभिन्‍नताएं

गूगल टूलबार

गूगल टूलबार की पेजरैंक विशेषता देखे गए पृष्ठ के पेजरैंक को 0 से 1 के बीच एक पूर्णांक संख्या के रूप में दर्शाती है। सर्वाधिक लोकप्रिय वेबसाइटों का पेजरैंक 10 होता है। सबसे कम का पेजरैंक 0 होता है। टूलबार पेजरैंक मान के निर्धारण की सटीक विधि को गूगल उजागर नहीं करता, पहले इसे http://www.google.com/search?client=navclient-auto&ch=6-1484155081&features=Rank&q=info:http://www.wikipedia.org/ पर जाकर देखा जा सकता था (ध्यान दें: 23.01.2010 तक की जानकारी के अनुसार यह लिंक सेवा-शर्तों के उल्लंघन के रूप में एक गूगल त्रुटि उत्पन्न करती है) जहां www.wikipedia.org वेबसाइट का नाम है।

एक पंक्ति का निम्नलिखित जावास्क्रिप्ट URL प्रतिस्थापन करता है और इसका प्रयोग किसी भी ब्राउज़र (गूगल क्रोम सहित, जिसमें अभी गूगल टूलबार एड-इन शामिल नहीं है) के बुकमार्क बार में बुकमार्कलेट के रूप में उपयोगी हो सकने के लिये किया जाता है।

javascript:location.href='http:\/\/www.google.com\/search?client=navclient-auto&ch=6-1484155081&features=Rank&q=info:'+encodeURIComponent(location.href);

(ध्यान दें: 10 सितंबर 2009 तक की जानकारी के अनुसार उपरोक्त दो तकनीकें 403 निषिद्ध त्रुटि उत्पन्न करती हैं)

गूगल टूलबार को वर्ष में लगभग 5 बार नवीनीकृत किया जाता है, अतः यह अक्सर पुराने मान प्रदर्शित करता है। अंतिम बार इसे 13/14 फ़रवरी 2010 को अद्यतन किया गया था।

SERP रैंक

SERP (सर्च इंजन रिज़ल्ट पेज) किसी मुख्य-शब्द की प्रतिक्रिया में सर्च इंजन द्वारा प्रदान किया गया वास्तविक परिणाम होता है। SERP में संबंधित पाठ्य-खण्डों वाले सभी वेब पृष्ठों के लिये लिंक्स की एक सूची होती है। किसी वेब पृष्ठ का SERP रैंक SERP पर संबंधित लिंक की स्थापना को सूचित करता है, जहां उच्च स्थापना का अर्थ है उच्च SERP रैंक. एक वेब पृष्ठ का SERP रैंक न केवल इसके पेजरैंक का एक फंक्शन होता है, बल्कि यह कारकों के अपेक्षाकृत बड़े और लगातार समायोजित होने वाले समुच्चय पर निर्भर होता है, जिसे इंटरनेट विपणनकर्ताओं द्वारा सामान्यतः "गूगल लव" कहा जाता है। SEO (सर्च इंजन ऑप्टिमाइज़ेशन) का लक्ष्य एक वेबसाइट या वेब पृष्ठों के समूह के लिये उच्चतम संभव SERP रैंक प्राप्त करना होता है।

गूगल डायरेक्ट्री पेजरैंक

गूगल डायरेक्ट्री पेजरैंक 8-इकाइयों वाला एक मापन है। इन मानों को गूगल डायरेक्ट्री में देखा जा सकता है। गूगल टूलबार, जो कि एक हरी पट्टिका पर माउस घुमाए जाने पर पेजरैंक मान दर्शाता है, के विपरीत गूगल डायरेक्ट्री पेजरैंक को एक अंकीय मान के रूप में नहीं, बल्कि केवल एक हरी पट्टिका के रूप में दर्शाता है।

असत्य या नकली पेजरैंक

हालांकि अधिकांश साइटों के लिये टूलबार में प्रदर्शित पेजरैंक को वास्तविक पेजरैंक मान (गूगल द्वारा प्रकाशन से कुछ समय पूर्व) से प्राप्त माना जाता है, परंतु इस बात पर ध्यान देना आवश्यक है कि इस मान को सरलता से बदल दिया जाता था। पिछला एक दोष यह था कि एक HTTP 302 प्रतिक्रिया या एक "रिफ़्रेश" मेटा टैग के द्वारा, उच्च पेजरैंक वाले किसी पेज की ओर भेजा जाने वाला निम्न पेजरैंक वाला कोई भी पृष्ठ गंतव्य पृष्ठ का पेजरैंक प्राप्त कर लेता था। सैद्धांतिक रूप से, कोई PR 0 पेज, जिसमें अंतर्गामी लिंक न हों, को गूगल के होम पेज की ओर भेजा जा सकता था- जिसका PR 10 है- और फिर वह नए पृष्ठ का PR उन्नत होकर PR10 हो जाता. स्पूफ़िंग की यह तकनीक, जिसे 302 गूगल जैकिंग भी कहा जाता है, प्रणाली में एक विफलता या त्रुटि के रूप में जानी जाती थी। वेबमास्टर की इच्छानुसार किसी भी पृष्ठ के पेजरैंक को बदला जा सकता है और केवल गूगल के पास ही पृष्ठ के वास्तविक पेजरैंक का अभिगम होता है। स्पूफ़िंग की पहचान सामान्यतः संदिग्ध पेजरैंक वाले URL के लिये एक गूगल खोज चलाकर की जाती है क्योंकि परिणाम एक पूर्णतः भिन्न साइट (जिसके ओर निर्देशित किया गया है) का URL प्रदर्शित करेंगे।

पेजरैंक में धोखाधड़ी करना

सर्च इंजन ऑप्टिमाइज़ेशन के उद्देश्य से कुछ कम्पनियां वेबमास्टरों को उच्च पेजरैंक वाले लिंक्स बेचने का प्रस्ताव देती हैं। चूंकि उच्च-PR वाले पृष्ठों से प्राप्त लिंक्स को अधिक मूल्यवान माना जाता है, अतः वे अधिक महंगे होते हैं। अधिक यातायात प्राप्त करने और वेबमास्टर की लिंक की लोकप्रियता को बढ़ाने के लिये उच्च गुणवत्ता वाले सामग्री पृष्ठों और प्रासंगिक साइटों पर लिंक विज्ञापनों को खरीदना एक प्रभावी और अर्थक्षम विपणन रणनीति हो सकती है। हालांकि गूगल ने सार्वजनिक रूप से वेबमास्टरों को चेतावनी दी है कि यदि वे पेजरैंक और सम्मान देने के उद्देश्य से लिंक्स को बेचते हैं या ऐसा करते हुए पाए गए, तो उनकी लिंक्स का अवमूल्यन किया जाएगा (अन्य पृष्ठों के पेजरैंक की गणना करते समय उन्हें उपेक्षित कर दिया जाएगा). लिंक्स खरीदने और बेचने की पद्धति वेबमास्टर समुदाय के बीच अत्यधिक बहस का विषय है। गूगल ने वेबमास्टरों को प्रायोजित लिंक्स पर nofollow HTML एट्रीब्यूट मान का प्रयोग करने की सलाह दी है। मैट कट्स के अनुसार, गूगल उन वेबमास्टरों के प्रति चिंतित है, जो तंत्र के साथ खिलवाड़ करने का प्रयास करते हैं और इसके कारण गूगल के सर्च परिणामों की गुणवत्ता और विश्वसनीयता को घटा देते हैं।

सुविचारित सर्फर मॉडल

मूल पेजरैंक ऐल्गरिदम तथाकथित यादृच्छिक सर्फर मॉडल को प्रतिबिम्बित करता है, जिसका अर्थ यह है कि किसी विशिष्ट पृष्ठ का पेजरैंक यादृच्छिक रूप से लिंक्स पर क्लिक करने पर उस पृष्ठ पर पहुंचने की सैद्धांतिक प्रायिकता से प्राप्त किया जाता है। हालांकि, वास्तविक प्रयोक्ता वेब का प्रयोग यादृच्छिक रूप से नहीं करते, बल्कि अपनी रुचि और उद्देश्य के अनुसार लिंक्स पर जाते हैं। एक पृष्ठ रैंकिंग मॉडल, जो किसी विशिष्ट पृष्ठ के महत्व को इस बात के एक फंक्शन के रूप में प्रतिबिम्बित करता है कि वास्तव में इसे कितने वास्तविक प्रयोक्ताओं द्वारा देखा गया, एक सुविचारित सर्फर मॉडल कहलाता है। गूगल टूलबार देखे गए प्रत्येक पृष्ठ की सूचना गूगल को भेजता है और ऐसा करके सुविचारित सर्फर मॉडल पर आधारित पेजरैंक गणना के लिये आधार प्रदान करता है। गूगल द्वारा स्पैमडेक्सिंग का मुक़ाबला करने के लिये nofollow एट्रीब्यूट के प्रयोग का दुष्प्रभाव यह है कि वेबमास्टर सामान्यतः इसका प्रयोग बहिर्गामी लिंक पर अपना स्वयं का पेजरैंक बढ़ाने के लिये करते हैं। इसके परिणामस्वरूप वेब क्रॉलरों के लिए अनुपालन हेतु वास्तविक लिंक की हानि होती है, जो यादृच्छिक सर्फर मॉडल पर आधारित मूल पेजरैंक ऐल्गरिदम को अविश्वसनीय बना देता है। प्रयोक्ताओं की ब्राउज़िंग आदतों के बारे में गूगल द्वारा प्रदान की गई जानकारी का विश्लेषण करना nofollow एट्रीब्यूट के कारण होने वाली सूचना की हानि की कुछ हद तक पूर्ति करता है। एक पृष्ठ का SERP रैंक, जो कि खोज के परिणामों में पृष्ठ की वास्तविक स्थिति का निर्धारण करता है, अन्य कारकों के अतिरिक्त यादृच्छिक सर्फर मॉडल (पेजरैंक) और सुविचारित सर्फर मॉडल (ब्राउज़िंग आदतों) के संयोजन पर आधारित होता है।

अन्य उपयोग

पेजरैंक का एक संस्करण हाल ही में पारंपरिक [[वैज्ञानिक सूचना संस्थान (Institute for Scientific Information [ISI])]] प्रभाव कारक के प्रतिस्थापन के रूप में प्रस्तावित किया गया है और इसे eigenfactor.org पर लागू किया गया है। केवल किसी पत्रिका के अवतरणों को गिनने की बजाय, एक पेजरैंक पद्धति से प्रत्येक अवतरण के "महत्व" का निर्धारण किया जाता है।

शैक्षणिक शोध कार्यक्रमों द्वारा उनके स्नातकों को प्राध्यापक पदों पर स्थापित करने के उनके रिकॉर्ड के आधार पर उन्हें रैंक देना पेजरैंक का इसी प्रकार का एक नया उपयोग है। पेजरैंक के संदर्भ में, शैक्षणिक विभाग एक दूसरे से (और स्वयं से) प्राध्यापकों को नौकरी देकर एक-दूसरे से जुड़े होते हैं।

पेजरैंक का प्रयोग स्थानों या सड़कों को रैंक देने के लिये किया जाता रहा है, ताकि इस बात का पूर्वानुमान लगाया जा सके कि किसी एक स्थान या सड़क पर कितने लोग (पैदल या वाहन) आते हैं।. शाब्दिक अर्थ विज्ञान में इसका प्रयोग शब्द अर्थ असंदिग्धता (Word Sense Disambiguation) और वर्डनेट सिनसेट्स (WordNet synsets) को इस आधार पर स्वचालित रूप से श्रेणीबद्ध करने के लिये किया जाता है कि उनमें कितनी मज़बूती से कोई अर्थ विज्ञान विशेषता, जैसे धनात्मकता या ऋणात्मकता, उपस्थित है।

पेजरैंक के समान ही एक अन्य गतिज भारण विधि का प्रयोग विकिपीडिया की लिंक संरचना पर आधारित पाठन सूचियों को रुचि के अनुसार निर्मित करने के लिये किया जाता रहा है।

एक वेब क्रॉलर पेजरैंक का प्रयोग इस बात के निर्धारण के अनेक महत्वपूर्ण मेट्रिक्स में से एक के रूप में कर सकता है कि वेब के एक क्रॉल के दौरान आगे किस URL पर जाना है। उन प्रारंभिक कार्य पत्रों में से एक, जिनका प्रयोग गूगल के निर्माण के दौरान किया गया था, Efficient crawling through URL ordering है , जो इस बात के निर्धारण के लिये विभिन्न महत्वपूर्ण मेट्रिक्स के प्रयोग पर चर्चा करता है कि गूगल कितनी गहराई तक और किसी साइट के कितने भाग तक क्रॉल करेगा। पेजरैंक को इन अनेक महत्वपूर्ण मेट्रिक्स में से एक के रूप में प्रस्तुत किया गया है, हालांकि कुछ अन्य भी सूचीबद्ध किये गए हैं, जैसे किसी URL के लिये अंतर्गामी और बहिर्गामी लिंक्स की संख्या और किसी साइट पर URL से मूल निर्देशिका तक की दूरी.

पेजरैंक का प्रयोग संपूर्ण वेब पर ब्लॉगस्फीयर जैसे किसी समुदाय के प्रकट प्रभाव का मापन करने की एक कार्य-पद्धति के रूप में भी किया जा सकता है। अतः यह दृष्टिकोण मापन-मुक्त नेटवर्क प्रतिमान के प्रतिबिम्ब में ध्यान के वितरण का मापन करने के लिये पेजरैंक का प्रयोग करता है।

किसी भी पारिस्थितिकी तंत्र में, पेजरैंक के एक संशोधित संस्करण का प्रयोग उन प्रजातियों के निर्धारण के लिये किया जा सकता है, जो वातावरण के स्वास्थ्य को बनाए रखने के लिये आवश्यक हों.

गूगल का rel

"nofollow" option== 2005 के प्रारंभ में, HTML लिंक और एंकर तत्व के rel एट्रीब्यूट के लिये, गूगल ने एक नया मान "nofollow" लागू किया, ताकि वेबसाइट विकासकर्ता और ब्लॉगर ऐसे लिंक बना सकें, जिन पर गूगल पेजरैंक के उद्देश्यों के लिये विचार नहीं करेगा- ये वे लिंक्स हैं, जो पेजरैंक प्रणाली में अब "मतदान" नहीं करते. nofollow संबंध को स्पैमडेक्सिंग से मुक़ाबला करने में सहायता के एक प्रयास के रूप में जोड़ा गया था।

एक उदाहरण के रूप में, अपने पेजरैंक को बढ़ाने के लिए लोग पहले ऐसे अनेक मैसेज-बोर्ड प्रविष्टियां बनाया करते थे, जिनमें उनकी वेबसाइटों के लिंक होते थे। nofollow मान के साथ, मैसेज-बोर्ड प्रविष्टियों में सभी हाइपरलिंक्स में स्वचालित रूप से "rel='nofollow'" प्रविष्ट करने के लिये प्रशासक अपने कोड को संशोधित कर सकते हैं और इस प्रकार पेजरैंक को उन विशिष्ट प्रविष्टियों द्वारा प्रभावित होने से बचाया जा सकता है। हालांकि, परिहार की इस विधि की विभिन्न कमियां भी हैं, जैसे वास्तविक टिप्पणियों के लिंक मान को घटाना. (देखें: blogs#nofollow में स्पैम)

किसी वेबसाइट के पृष्ठों के अंतर्गत पेजरैंक के प्रवाह को मानवीय रूप से नियंत्रित करने के एक प्रयास में, अनेक वेबमास्टर पेजरैंक स्कल्पटिंग नामक पद्धति का प्रयोग करते हैं- जो कि nofollow एट्रीब्यूट को रणनीतिक रूप से वेबसाइट के विशिष्ट आंतरिक लिंक्स पर रखने का कार्य है, ताकि पेजरैंक को उन पृष्ठों की ओर मोड़ा जा सके, जिन्हें वेबमास्टर सबसे महत्वपूर्ण मानता है। इस चाल का प्रयोग nofollow एट्रीब्यूट के जन्म के समय से किया जा रहा है, लेकिन अनेक व्यक्ति मानते हैं कि यह तकनीक अपनी प्रभावकारिता खो चुकी है।

गूगल वेबमास्टर टूल्स से हटाया जाना

14 अक्टूबर 2009 को गूगल के कर्मचारी सुज़ैन मोस्क्वा ने पुष्टि की कि कम्पनी ने पेजरैंक को अपने वेबमास्टर टूल्स खण्ड से हटा दिया है। उनकी प्रविष्टि ने आंशिक रूप से कहा कि "हम लंबे समय से लोगों को बता रहे हैं कि उन्हें पेजरैंक पर इतना अधिक ध्यान केंद्रित नहीं करना चाहिये; ऐसा प्रतीत होता है कि अनेक साइट मालिक सोचते हैं कि यह उनके लिये सबसे महत्वपूर्ण मापन है, जो कि सत्य नहीं है।" मोस्क्वा की पुष्टि के दो दिनों बाद तक भी पेजरैंक को गूगल टूलबार के वेब उपकरणों पर प्रदर्शित किया जाता रहा और मार्च 2010 तक की जानकारी के अनुसार यह अभी भी प्रदर्शित हो रहा है।

इन्हें भी देखें

• आइजनट्रस्ट - एक विकेन्द्रीकृत पेजरैंक ऐल्गरिदम
• हिलटॉप ऐल्गरिदम
• लिंक लव
• पिजनरैंक
• पॉवर विधि - पेजरैंक की गणना के लिए दोहरावपूर्ण आइजन्वेक्टर ऐल्गरिदम
• सर्च इंजन इष्टतमीकरण
• सिमरैंक - यादृच्छिक सर्फर मॉडल पर आधारित वस्तु दर वस्तु की समानता
• ट्रस्टरैंक

सन्दर्भ

• Altman, Alon; Moshe Tennenholtz (2005). "Ranking Systems: The PageRank Axioms" (PDF). Proceedings of the 6th ACM conference on Electronic commerce (EC-05). Vancouver, BC. Archived from the original on 30 मई 2008. https://web.archive.org/web/20080530174108/http://stanford.edu/~epsalon/pagerank.pdf. अभिगमन तिथि: 2008-02-05. 
• Cheng, Alice; Eric J. Friedman (2006-06-11). "Manipulability of PageRank under Sybil Strategies" (PDF). Proceedings of the First Workshop on the Economics of Networked Systems (NetEcon06). Ann Arbor, Michigan. Archived from the original on 21 अगस्त 2010. https://web.archive.org/web/20100821011759/http://www.cs.duke.edu/nicl/netecon06/papers/ne06-sybil.pdf. अभिगमन तिथि: 2008-01-22. 
• Farahat, Ayman; LoFaro, Thomas; Miller, Joel C.; Rae, Gregory and Ward, Lesley A. (2006). "Authority Rankings from HITS, PageRank, and SALSA: Existence, Uniqueness, and Effect of Initialization". SIAM Journal on Scientific Computing. 27 (4): 1181–1201.सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)
• Haveliwala, Taher; Jeh, Glen and Kamvar, Sepandar (2003). "An Analytical Comparison of Approaches to Personalizing PageRank" (PDF). Stanford University Technical Report. Archived from the original on 16 दिसंबर 2010. https://web.archive.org/web/20101216084254/http://www-cs-students.stanford.edu/~taherh/papers/comparison.pdf. अभिगमन तिथि: 25 जून 2010. 
• Langville, Amy N.; Meyer, Carl D. (2003). "Survey: Deeper Inside PageRank". Internet Mathematics. 1 (3).
• Langville, Amy N.; Meyer, Carl D. (2006). Google's PageRank and Beyond: The Science of Search Engine Rankings. Princeton University Press. आई॰ऍस॰बी॰ऍन॰ 0-691-12202-4.
• Page, Lawrence; Brin, Sergey; Motwani, Rajeev and Winograd, Terry (1999). "The PageRank citation ranking: Bringing order to the Web". मूल से 27 अप्रैल 2006 को पुरालेखित. अभिगमन तिथि 25 जून 2010. सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)
• Richardson, Matthew; Domingos, Pedro (2002). "The intelligent surfer: Probabilistic combination of link and content information in PageRank" (PDF). Proceedings of Advances in Neural Information Processing Systems. 14. Archived from the original on 28 जून 2010. https://web.archive.org/web/20100628120615/http://www.cs.washington.edu/homes/pedrod/papers/nips01b.pdf. अभिगमन तिथि: 25 जून 2010. 

बाहरी कड़ियाँ

• गूगल द्वारा आवॉर सर्च: गूगल टेक्नालजी
• अमेरिकी गणितीय सोसाइटी द्वारा हाउ गूगल फाइंड्स यॉर नीडल इन द वेब्स हेयस्टैक
• इन्फोग्राफिक गूगल कैसे क्रॉल और इंडेक्स करता है वेबसाइट को
• मूल पेजरैंक अमेरिकी पेटेंट - लिंक्ड डेटाबेस में नोड रैंकिंग की विधि - 4 सितम्बर 2001
• पेजरैंक अमेरिकी पेटेंट - लिंक्ड डेटाबेस में दस्तावेजों के हिसाब की विधि Archived 2021-02-24 at the वेबैक मशीन - 28 सितम्बर 2004
• पेजरैंक अमेरिकी पेटेंट - लिंक्ड डेटाबेस में नोड रैंकिंग की विधि Archived 2019-08-28 at the वेबैक मशीन - 6 जून 2006
• पेजरैंक अमेरिकी पेटेंट - लिंक्ड डेटाबेस में दस्तावेजों के हिसाब की विधि Archived 2018-03-31 at the वेबैक मशीन - 11 सितम्बर 2007
• वैज्ञानिक पेजरैंक को खोजते है-1940 से एक प्रकार का ऐल्गरिदम Archived 2010-05-29 at the वेबैक मशीन - 17 फ़रवरी 2010