मंडेलब्रॉट सेट[संपादित करें]

मंडेलब्रॉट सेट जटिल संख्याओं का सेट है $c$ जिसके लिए फ़ंक्शन $f_{c}(z)=z^{2}+c$ $z=0$ , यानी अनुक्रमित होने पर विचलित नहीं होता है, जिसके लिए अनुक्रम $f_{c}(0)$ , $f_{c}(f_{c}(0))$ , आदि, निरपेक्ष मूल्य में घिरा रहता है।

इसकी परिभाषा और नाम गणितज्ञ बेनोइट मैंडलब्रॉट के सम्मान में,एड्रियान डौडी के कारण हैं। मंडेलब्रॉट सेट जूलिया सेट से जुड़ा हुआ है, और संबंधित जूलिया सेट इसी तरह के जटिल फ्रैक्टल आकार उत्पन्न करते हैं।

मैंडेलब्रॉट सेट छवियों, जटिल संख्याओं और परीक्षण के नमूने प्रत्येक नमूने बिंदु $c$ के द्वारा बनाया जा सकता हे, चाहे अनुक्रम $f_{c}(0),f_{c}(f_{c}(0)),\dotsc$ अनंत तक जाता है। जटिल विमान पर छवि निर्देशांक के रूप में $c$ के वास्तविक और काल्पनिक हिस्सों का इलाज करते हुए, पिक्सेल को तब अनुक्रमित किया जा सकता है जब अनुक्रम $|f_{c}(0)|,|f_{c}(f_{c}(0))|,\dotsc$ एक विशेष रूप से चुने गए थ्रेसहोल्ड को पार करता है, विशेष के साथ रंग (आमतौर पर काला) $c$ के मानों के लिए उपयोग किया जाता है जिसके लिए अनुक्रम की पूर्व निर्धारित संख्या के बाद अनुक्रम पार नहीं किया गया है (मंडलब्रॉट सेट छवि को इसके पूरक की छवि से स्पष्ट रूप से अलग करना आवश्यक है)। यदि $c$ निरंतर बना दिया गया है और $z$ का प्रारंभिक मान ( $z_{0}$ द्वारा निर्दिष्ट किया गया है) यह चर है,पैरामीटर स्पेस में सरल प्रदर्शन के साथ प्रत्येक बिंदु, $c$ के लिए संबंधित जूलिया सेट प्राप्त करते है।

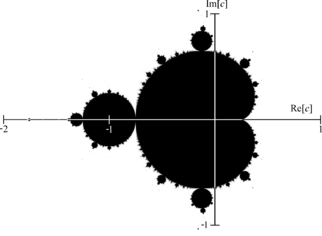
मंडेलब्रॉट सेट की छवियां एक विस्तृत और असीमित जटिल सीमा प्रदर्शित करती हैं जो बढ़ती आवर्धन पर प्रगतिशील रूप से कभी-कभी रिकर्सिव विस्तार से पता चलता है। इस दोहराने वाले विवरण की "शैली" सेट की जांच के क्षेत्र पर निर्भर करती है। सेट की सीमा मुख्य आकार के छोटे संस्करणों को भी शामिल करती है, इसलिए आत्म-समानता की फ्रैक्टल संपत्ति पूरे सेट पर लागू होती है, न कि केवल इसके हिस्सों में।

मंडेलब्रॉट सेट केवल अपने सौंदर्य अपील के लिए गणित के बाहर लोकप्रिय हो गया है बल्कि यह सरल नियमों के आवेदन से उत्पन्न जटिल संरचना का एक उदाहरण भी है। यह गणितीय दृश्यता और गणितीय सौंदर्य के सबसे प्रसिद्ध उदाहरणों में से एक है।

इतिहास[संपादित करें]

1978 में रॉबर्ट डब्ल्यू ब्रूक्स और पीटर मैटलस्की द्वारा मंडेलब्रॉट सेट की पहली प्रकाशित तस्वीर

मंडेलब्रॉट सेट जटिल गतिशीलता का एक हिस्सा है, जो २० वीं शताब्दी की शुरुआत में फ्रांसीसी गणितज्ञ पियरे फाटो और गैस्टन जूलिया द्वारा पहली बार जांच की गई थी। इस फ्रैक्टल को पहली बार क्लेनीन समूहों के अध्ययन के हिस्से के रूप में रॉबर्ट डब्ल्यू ब्रूक्स और पीटर मैटलस्की द्वारा १९७८ में परिभाषित और तैयार किया गया था। पर 1 मार्च 1980, यॉर्कटाउन हाइट्स आईबीएम के थॉमस जे वाटसन रिसर्च सेंटर, न्यूयॉर्क में, बेनोइट मैंडलब्रॉट पहले सेट के एक दृश्य देखा।

मंडेलब्रॉट ने १९८० में प्रकाशित एक लेख में वर्गबद्ध बहुपदों के पैरामीटर स्पेस का अध्ययन किया। मंडेलब्रॉट सेट का गणितीय अध्ययन गणितज्ञ एड्रियान डौडी और जॉन एच। हूबार्ड के काम से शुरू हुआ, जिन्होंने अपनी कई मौलिक संपत्तियों की स्थापना की और सेट का नाम मंडेलब्रॉट के नाम पर रखा, उनकी फ्रैक्टल ज्यामिति के क्षेत्र मे योगदान को द्यान मे रक्ते हुए। गणितज्ञ हेनज़-ओटो पित्जेन और पीटर रिक्टर फोटोग्राफ, किताबें, और जर्मन गोएथे-इंस्टिट्यूट के अंतरराष्ट्रीय स्तर पर दौरे के प्रदर्शन के साथ सेट को बढ़ावा देने के लिए जाने जाते हैं।

अगस्त १९८५ के वैज्ञानिक लेख के कवर आलेख ने मंडलब्रॉट सेट को व्यापक दर्शकों के साथ कंप्यूटिंग करने के लिए एल्गोरिदम प्रस्तुत किया। कवर में -०.९०९ + -०.२७५ पर स्थित एक छवि शामिल है और इसे पिटजेन द्वारा बनाया गया था। मंडलब्रॉट सेट १९८० के दशक के मध्य में कंप्यूटर ग्राफिक्स डेमो के रूप में प्रमुख बन गया, जब निजी कंप्यूटर उच्च संकल्प में सेट को प्लॉट करने और प्रदर्शित करने के लिए पर्याप्त शक्तिशाली बन गए।

डौडी और हूबार्ड के काम में जटिल गतिशीलता और अमूर्त गणित में रुचि में भारी वृद्धि हुई, और मंडलब्रॉट सेट का अध्ययन तब से इस क्षेत्र का केंद्रबिंदु रहा है। तब से इस सेट की समझ में योगदान देने वाले सभी लोगों की एक सूची लंबी है, लेकिन इसमें मिखाइल ल्यूबिक, कर्ट मैकमुलेन, जॉन मिलनर, मित्सुहिरो शिशिकुरा और जीन-क्रिस्टोफ योकोज़ शामिल होंगे।

औपचारिक परिभाषा[संपादित करें]

मंडेलब्रॉट सेट जटिल विमान में c के मूल्यों का सेट है जिसके लिए चौकोर मानचित्र के पुनरावृत्ति के तहत 0 की कक्षा

z_{n+1}=z_{n}^{2}+c

बनी हुई है। यानी, एक जटिल संख्या सी मंडेलब्रॉट सेट का हिस्सा है, यदि z₀ = 0 से शुरू होता है और पुनरावृत्ति को बार-बार लागू करता है, तो z_n का पूर्ण मूल्य बनी रहती है हालांकि बड़ी n हो जाती है। इसका भी प्रतिनिधित्व किया जा सकता है

z_{n+1}=z_{n}^{2}+c,

c\in M\iff \limsup _{n\to \infty }|z_{n+1}|\leq 2.

उदाहरण के लिए, c= 1 अनुक्रम 0, 1, 2, 5, 26, ... देता है, जो अनंतता तक रहता है। चूंकि यह अनुक्रम असंबद्ध है, 1 मंडेलब्रॉट सेट का एक तत्व नहीं है। दूसरी ओर, सी = -1 अनुक्रम 0, -1, 0, -1, 0, ... देता है, जो बाध्य है, और इसलिए -1 मंडेलब्रॉट सेट से संबंधित है।

मैंडलब्रॉट सेट $M$ को जटिल द्विघात बहुपद के एक परिवार द्वारा परिभाषित किया जा सकता है

P_{c}:\mathbb {C} \to \mathbb {C}

द्वारा दिए गए

P_{c}:z\mapsto z^{2}+c,

जहाँ $c$ एक जटिल पैरामीटर है। प्रत्येक $c$ के लिए, एक अनुक्रम के व्यवहार को मानता है

(0,P_{c}(0),P_{c}(P_{c}(0)),P_{c}(P_{c}(P_{c}(0))),\ldots )

पुनरावृत्ति द्वारा प्राप्त $P_{c}(z)$ महत्वपूर्ण बिंदु पर शुरू $z=0$ , जो या तो अनंत को निकल जाता है या कुछ परिमित त्रिज्या का एक डिस्क के अंदर रहता है । मैंडलब्रॉट सेट को सभी बिंदुओं के सेट के रूप में परिभाषित किया गया है $c$ जैसे कि उपरोक्त अनुक्रम अनंत तक नहीं जाता है।

अधिक औपचारिक रूप से, यदि $P_{c}^{n}(z)$ $P_{c}(z)$ के nth पुनरावृति को दर्शाता है (अर्थात $P_{c}(z)$ स्वयं n समय से बना), मंडेलब्रॉट सेट द्वारा दिए गए जटिल विमान का सबसेट है

M=\left\{c\in \mathbb {C} \mid (\exists s\in \mathbb {R} ^{+})(\forall n\in \mathbb {N} )(|P_{c}^{n}(0)|\leq s)\right\}.

जैसा कि नीचे बताया गया है, वास्तव में $s=2$ लेकर इस परिभाषा को सरल बनाना संभव है। गणितीय रूप से, मैंडलब्रॉट सेट जटिल संख्याओं का एक सेट है। एक दिया गया जटिल नंबर c या तो M का है या नहीं। मैंडलब्रॉट सेट की एक तस्वीर को सभी बिंदुओं $c$ जो कि M ब्लैक से संबंधित है, और अन्य सभी बिंदुओं को सफेद करके बनाया जा सकता है। आमतौर पर देखी जाने वाली अधिक रंगीन तस्वीरें उस बिंदु के अनुसार सेट में नहीं रंग के बिंदुओं से उत्पन्न होती हैं $|P_{c}^{n}(0)|$ एक निश्चित कटऑफ से अधिक पूर्ण मूल्य वाला पहला शब्द है। मूल्य, आमतौर पर 2. उपयोग किए जाने वाले रंगों की सूची हमेशा उपयोगकर्ता द्वारा उपयोग किए गए या बनाए गए प्रोग्राम द्वारा पूर्वनिर्धारित की जाती है, सूची में अगला रंग चुना जाता है जब पुनरावृत्ति गिनती बढ़ती है।

मैंडेलब्रोट सेट को बहुपद के परिवार के संयोजी स्थान के रूप में भी परिभाषित किया जा सकता है। बहुपद $P_{c}(z)$ । यही है, यह उन मापदंडों से मिलकर जटिल विमान का सबसेट है $c$ जिसके लिए जूलिया का सेट $P_{c}$ जुड़ा हुआ स्थान है|

$P_{c}^{n}(0)$ c में एक बहुपद है और इसके प्रमुख शब्द n के रूप में बड़े होते हैं। ये शब्द कैटलन संख्याओं द्वारा दिए गए हैं। बहुपत्नी $P_{c}^{n}(0)$ कैटलन संख्याओं के लिए जनरेटिंग फंक्शन से बंधे होते हैं और n में अनंत तक जाते हैं।

मूल गुण[संपादित करें]

मैंडेलब्रॉट सेट एक कॉम्पैक्ट सेट है, क्योंकि यह मूल के आसपास त्रिज्या 2 के बंद डिस्क में निहित और बंद है। अधिक विशेष रूप से, एक बिंदु $c$ अगर और केवल अगर मैंडेलब्रॉट सेट के अंतर्गत आता है

|P_{c}^{n}(0)|\leq 2

for all

n\geq 0.

दूसरे शब्दों में, यदि निरपेक्ष मान का < $P_{c}^{n}(0)$ कभी 2 से बड़ा हो जाता है, तो क्रम कम समय में अनंत तक पहुंच जाएगा।

मंडेलब्रोट सेट और लॉजिस्टिक मैप के द्विभाजन आरेख के बीच पत्राचार

चौराहा (सेट सिद्धांत) | वास्तविक धुरी के साथ $M$ का चौराहा ठीक अंतराल [-2, 1/4] है। इस अंतराल के साथ मापदंडों को वास्तविक लॉजिस्टिक मानचित्र के साथ एक-से-एक पत्राचार में रखा जा सकता है।

z\mapsto \lambda z(1-z),\quad \lambda \in [1,4].

पत्राचार इस प्रकार दिया गया है

c={\frac {\lambda }{2}}\left(1-{\frac {\lambda }{2}}\right).

वास्तव में, यह लॉजिस्टिक परिवार के पूरे पैरामीटर स्पेस और मैंडलब्रॉट सेट के बीच एक पत्राचार देता है।

डौडी और हबर्ड ने दिखाया है कि मैंडलब्रॉट सेट जुड़ा हुआ है। वास्तव में, उन्होंने मैंडलब्रॉट सेट के पूरक और बंद इकाई डिस्क के पूरक के बीच एक स्पष्ट अनुरूप समरूपता का निर्माण किया। मैंडलब्रॉट ने मूल रूप से अनुमान लगाया था कि मैंडेलब्रॉट सेट को काट दिया गया है। यह अनुमान उन प्रोग्रामों द्वारा उत्पन्न कंप्यूटर चित्रों पर आधारित था जो $M$ . के विभिन्न भागों को जोड़ने वाले पतले फिलामेंट का पता लगाने में असमर्थ हैं। आगे के प्रयोगों पर, उन्होंने अपने अनुमान को संशोधित करते हुए, यह निर्णय लिया कि $M$ कनेक्ट होना चाहिए। जेरेमी कहन द्वारा 2001 में खोज की गई कनेक्टिविटी के लिए एक सामयिक प्रमाण भी मौजूद है।

मंडेलब्रॉट सेट में 1 महाद्वीप की अवधि के पास जागने की बाहरी किरणें डौडी और हबर्ड के $M$ की कनेक्टिविटी के प्रमाण से उत्पन्न मंडेलब्रोट सेट के पूरक की एकरूपता के लिए गतिशील सूत्र, मैंडेलब्रो सेट की बाहरी किरणों को जन्म देता है। इन किरणों का उपयोग कॉम्बिनेटरियल शब्दों में सेट मेंडेलब्रोट का अध्ययन करने के लिए किया जा सकता है और योकोज़ पैरापॉज़ की रीढ़ बन सकता है।

सन्दर्भ[संपादित करें]

https://en.wikipedia.org/wiki/Mandelbrot_set

http://mathworld.wolfram.com/MandelbrotSet.html

https://plus.maths.org/content/what-mandelbrot-set