व्यावहारिक गणित

व्यावहारिक गणित (अनुप्रयुक्त गणित या प्रायोगिक गणित), गणित की वह शाखा है जो ज्ञान की अन्य विधाओं की समस्याओं को गणित के जुगाड़ों (तकनीकों) के प्रयोग से हल करने से सम्बन्ध रखती है। ऐतिहास दृष्टि से देखें तो भौतिक विज्ञानों (physical sciences) की आवश्यकताओं ने गणित की विभिन्न शाखाओं के विकास में महती भूमिका निभायी। उदाहरण के लिये तरल यांत्रिकी में गणित का उपयोग करने से एक हल्का एवं कम ऊर्जा से की खपत करने वाला वायुयान की डिजाइन की जा सकती है।
बहुत पुरातन काल से ही विषयों में गणित सर्वाधिक उपयोगी रहा है। यूनानी लोग गणित को न केवल संख्याओं और दिक् (स्पेस) का बल्कि खगोलविज्ञान और संगीत का भी अध्ययन मानते थे....।

गणितसारसंग्रह के 'संज्ञाधिकार' में मंगलाचरण के पश्चात महान प्राचीन भारतीय गणितज्ञ महावीराचार्य ने बड़े ही मार्मिक ढंग से गणित की प्रशंशा की है और गणित के अनेकानेक उपयोगों को गिनाया है-
- लौकिके वैदिके वापि तथा सामयिकेऽपि यः।
- व्यापारस्तत्र सर्वत्र संख्यानमुपयुज्यते॥
- कामतन्त्रेऽर्थशास्त्रे च गान्धर्वे नाटकेऽपि वा।
- सूपशास्त्रे तथा वैद्ये वास्तुविद्यादिवस्तुसु॥
- छन्दोऽलंकारकाव्येषु तर्कव्याकरणादिषु।
- कलागुणेषु सर्वेषु प्रस्तुतं गणितं परम्॥
- सूर्यादिग्रहचारेषु ग्रहणे ग्रहसंयुतौ।
- त्रिप्रश्ने चन्द्रवृत्तौ च सर्वत्रांगीकृतं हि तत्॥
- द्वीपसागरशैलानां संख्याव्यासपरिक्षिपः।
- भवनव्यन्तरज्योतिर्लोककल्पाधिवासिनाम्॥
- नारकाणां च सर्वेषां श्रेणीबन्धेन्द्रकोत्कराः।
- प्रकीर्णकप्रमाणाद्या बुध्यन्ते गणितेन् ते॥
- प्राणिनां तत्र संस्थानमायुरष्टगुणादयः।
- यात्राद्यास्संहिताद्याश्च सर्वे ते गणिताश्रयाः॥
- बहुभिर्प्रलापैः किं त्रैलोक्ये सचराचरे।
- यत्किंचिद्वस्तु तत् सर्वं गणितेन् बिना न हि॥
- लौकिके वैदिके वापि तथा सामयिकेऽपि यः।
- व्यापारस्तत्र सर्वत्र संख्यानमुपयुज्यते॥
- अर्थ: लौकिक, वैदिक तथा सामयिक में जो व्यापार है वहाँ सर्वत्र संख्या का ही उपयोग होता है। कामशास्त्र, अर्थशास्त्र, गन्धर्वशास्त्र, गायन, नाट्यशास्त्र, पाकशास्त्र, आयुर्वेद, छन्द, अलंकार, काव्य, तर्क, व्याकरण आदि में तथा कलाओं में समस्त गुणों में गणित अत्यन्त उपयोगी है। सूर्य आदि ग्रहों की गति ज्ञात करने में, देश और काल को ज्ञात करने में सर्वत्र गणित अंगीकृत है। द्वीपों, समूहों और पर्वतों की संख्या, व्यास और परिधि, लोक, अन्तर्लोक, स्वर्ग और नरक के निवासी, सब श्रेणीबद्ध भवनों, सभा एवं मन्दिरों के निर्माण गणित की सहायता से ही जाने जाते हैं। अधिक कहने से क्या प्रयोजन? तीनों लोकों में जो भी वस्तुएँ हैं उनका अस्तित्व गणित के बिना नहीं हो सकता।
आज के 4000 वर्ष पहले बेबीलोन तथा मिस्र सभ्यताएँ गणित का इस्तेमाल पंचांग (कैलेंडर) बनाने के लिए किया करती थीं जिससे उन्हें पूर्व जानकारी रहती थी कि कब फसल की बुआई की जानी चाहिए या कब नील नदी में बाढ़ आएगी। अंकगणित का प्रयोग व्यापार में रुपयों-पैसों और वस्तुओं के विनिमय या हिसाब-किताब रखने के लिए किया जाता था। ज्यामिति का इस्तेमाल खेतों के चारों तरफ की सीमाओं के निर्धारण तथा पिरामिड जैसे स्मारकों के निर्माण में होता था।
अपने दैनिक जीवन में रोजाना ही हम गणित का इस्तेमाल करते हैं-उस वक्त जब समय जानने के लिए हम घड़ी देखते हैं, अपने खरीदे गए सामान या खरीदारी के बाद बचने वाली रेजगारी का हिसाब जोड़ते हैं या फिर फुटबाल टेनिस या क्रिकेट खेलते समय बनने वाले स्कोर का लेखा-जोखा रखते हैं।
व्यवसाय और उद्योगों से जुड़ी लेखा संबंधी संक्रियाएं गणित पर ही आधारित हैं। बीमा (इंश्योरेंस) संबंधी गणनाएं तो अधिकांशतया ब्याज की चक्रवृद्धि दर पर ही निर्भर है। जलयान या विमान का चालक मार्ग के दिशा-निर्धारण के लिए ज्यामिति का प्रयोग करता है। सर्वेक्षण का तो अधिकांश कार्य ही त्रिकोणमिति पर आधारित होता है। यहां तक कि किसी चित्रकार के आरेखण कार्य में भी गणित मददगार होता है, जैसे कि संदर्भ (पर्सपेक्टिव) में जिसमें कि चित्रकार को त्रिविमीय दुनिया में जिस तरह से इंसान और वस्तुएं असल में दिखाई पड़ते हैं, उन्हीं का तदनुरूप चित्रण वह समतल धरातल पर करता है।
संगीत में स्वरग्राम तथा संनादी (हार्मोनी) और प्रतिबिंदु (काउंटरपाइंट) के सिद्धांत गणित पर ही आश्रित होते हैं। गणित का विज्ञान में इतना महत्व है तथा विज्ञान की इतनी शाखाओं में इसकी उपयोगिता है कि गणितज्ञ एरिक टेम्पल बेल ने इसे ‘विज्ञान की साम्राज्ञी और सेविका’ की संज्ञा दी है। किसी भौतिकविज्ञानी के लिए अनुमापन तथा गणित का विभिन्न तरीकों का बड़ा महत्व होता है। रसायनविज्ञानी किसी वस्तु की अम्लीयता को सूचित करने वाले पी एच (pH) मान के आकलन के लिए लघुगणक का इस्तेमाल करते हैं। कोणों और क्षेत्रफलों के अनुमापन द्वारा ही खगोलविज्ञानी सूर्य, तारों, चंद्र और ग्रहों आदि की गति की गणना करते हैं। प्राणीविज्ञान में कुछ जीव-जन्तुओं के वृद्धि-पैटर्नों के विश्लेषण के लिए विमीय विश्लेषण की मदद ली जाती है।
जैसे-जैसे खगोलीय तथा काल मापन संबंधी गणनाओं की प्रामाणिकता में वृद्धि होती गई, वैसे-वैसे नौसंचालन भी आसान होता गया तथा क्रिस्टोफर कोलम्बस और उसके परवर्ती काल से मानव सुदूरगामी नए प्रदेशों की खोज में घर से निकल पड़ा। साथ ही, आगे के मार्ग का नक्शा भी वह बनाता गया। गणित का उपयोग बेहतर किस्म के समुद्री जहाज, रेल के इंजन, मोटर कारों से लेकर हवाई जहाजों के निर्माण तक में हुआ है। राडार प्रणालियों की अभिकल्पना तथा चांद और ग्रहों आदि तक अन्तरिक्ष यान भेजने में भी गणित से काम लिया गया है।
व्यावहारिक गणित के कुछ क्षेत्र[संपादित करें]
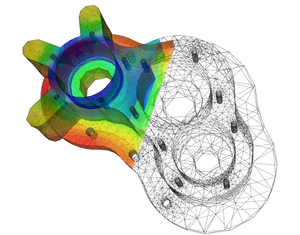
गणित के वे क्षेत्र जो बहुत अधिक अनुप्रयोगत्मक हैं, नीचे दिये गये हैं-
- चलन कलन तथा समाकलन (Differential and Integral Calculus)
- संख्यात्मक विश्लेषण
- रैखिक बीजगणित (लिनियर अल्जेब्रा)
- सम्मिश्र विश्लेषण और समिश्र चर
- फलन विश्लेषण & लाई बीजगणित (Lie algebra)
- अवकल समीकरण (differential equations)
- आनुमानिक सांख्यिकी (Inferential statistics)
- संक्रिया विज्ञान (operations research)
- विविक्त गणित (discrete mathematics)
- इष्टतमकरण (optimization)
- गतिकीय तन्त्र (dynamical systems)
- नियंत्रण सिद्धान्त (कन्ट्रोल थिअरी)
- प्रायिकता सिद्धान्त (Probability theory)
- फ्रैक्टल (Fractal)
- तरल यांत्रिकी
- प्रकाशिकी एवं विद्युतचुम्बकीय सिद्धान्त
- उष्मागतिकी एवं उष्मा स्थानान्तरण (thermodynamics, heat transfer)
- सांख्यिकीय यांत्रिकी (Statistical mechanics)
- पदार्थ की संरचना
- सापेक्षिकता एवं गुरुत्व सिद्धान्त
- खगोल विज्ञान (Astronomy and astrophysics)
- तंत्र सिद्धान्त एवं नियंत्रण सिद्धान्त (Systems theory)
- जीवविज्ञान
- खेल सिद्धान्त (Game theory)
इन्हें भी देखें[संपादित करें]
- शुद्ध गणित (Pure mathematics)
- अभिकलनात्मक गणित (computational mathematics)
- व्यावहारिक विज्ञान
- व्यावहारिक भौतिकी
