संधारित्र

विभिन्न तरह के आधुनिक संधारित्र

संधारित्र या कैपेसिटर (Capacitor), विद्युत परिपथ में प्रयुक्त होने वाला दो सिरों वाला एक प्रमुख अवयव है। संधारित्र में धातु की दो प्लेटें होतीं हैं जिनके बीच के स्थान में कोई कुचालक डाइएलेक्ट्रिक पदार्थ (जैसे कागज, पॉलीथीन, माइका आदि) भरा होता है। संधारित्र के प्लेटों के बीच धारा का प्रवाह तभी होता है जब इसके दोनों प्लेटों के बीच का विभवान्तर समय के साथ बदले। इस कारण नियत डीसी विभवान्तर लगाने पर स्थायी अवस्था में संधारित्र में कोई धारा नहीं बहती। किन्तु संधारित्र के दोनो सिरों के बीच प्रत्यावर्ती विभवान्तर लगाने पर उसके प्लेटों पर संचित आवेश कम या अधिक होता रहता है जिसके कारण वाह्य परिपथ में धारा बहती है। संधारित्र से होकर डीसी धारा नही बह सकती।

संधारित्र की धारा और उसके प्लेटों के बीच में विभवान्तर का सम्बन्ध निम्नांकित समीकरण से दिया जाता है-

$I = C{dU\over dt}$

जहाँ :

• I संधारित्र के प्लेटों के बीच बहने वाली धारा है,
• U संधारित्र के प्लेटों के बीच का विभवान्तर है,
• C संधारित्र की धारिता है जो संधारित्र के प्लेटों की दूरी, उनके बीच प्रयुक्त डाइएलेक्ट्रिक पदार्थ, प्लेटों का क्षेत्रफल एवं अन्य ज्यामितीय बातों पर निर्भर करता है। संधारित्र की धारिता निम्नलिखित समीकरण से परिभाषित है-

$Q = C \cdot U$

संधारित्रों के प्रमुख उपयोग

• उर्जा भण्डारण के लिये
• शक्ति गुणांक को बेहतर बनाने के लिये
• विभिन्न विद्युत फिल्टरों में
• विद्युत परिपथों में समय-सम्बन्धी परिपथ (timing circuit) बनाने के लिये
• पल्स-पॉवर एवं शस्त्र निर्माण
• सेंसर के रूप में (जैसे CVT = कैपेसिटिव वोल्टेज ट्रांसफॉर्मर)

संधारित्रों का संयोजन

जिस प्रकार प्रतिरोधों और प्रेरकत्वों को आवश्यकतानुसार श्रेणीक्रम या समान्तर क्रम में जोड़कर उचित मान (वैल्यू) तथा उचित रेटिंग (वाटेज, वोल्टता, धारा की रेटिंग आदि) प्राप्त कर ली जाती है, उसी प्रकार दो या अधिक संधारित्रों को भी आवश्यकतानुसार संयोजित किया जाता है।

श्रेणीक्रम में संयोजन

श्रेणीक्रम में जुड़े हुए n संधारित्रों का तुल्य धारिता निम्नलिखित सूत्र से दी जाती है:

${1 \over C_z}={1 \over C_1}+{1 \over C_2}+...+{1 \over C_n} = \sum_{i=1}^{n} {1 \over C_i}$

दो संधारित्र श्रेणीक्रम में जोड़े जाँय तो उनकी तुल्य धारिता निम्नलिखित सरल सूत्र से निकाला जा सकता है-

$C_z={C_{1}C_{2} \over C_{1}+C_{2}}$

और अगर दोनो संधारित्र समान मान वाले हों तो श्रेणीक्रम में संयोजित करने पर उनकी तुल्य धारिता प्रत्येक की धारिता की आधी हो जाती है। उदाहरण के लिये १० माइक्रोफैराड के दो संधारित्रों को श्रेणीक्रम में जोड़ने पर तुल्य धारिता ५ माइक्रोफैराड होगी।

समान्तरक्रम में संयोजन

समान्तर क्रम में जुड़े संधारित्रों की कुल धारिता (तुल्य धारिता) उनकी धारिताओं के योग के बराबर होती है।

$C_{z}=C_{1}+C_{2}+...+C_{n}=\sum_{i=1}^{n}C_{i}$

उदाहरण के लिये १० माइक्रोफैराड वाले ४ संधारित्र समान्तरक्रम में जोड़ दिये जाँय तो उनकी कुल धारिता ४० माइक्रोफैराड हो जाएगी।

कुछ प्रमुख संधारित्र संरचनाएं

संधारित्र की दो प्लेटों (चालकों) का संयोजन (अरेंजमेन्ट) तरह-तरह से किया जा सकता है। इस प्रकार संधारित्र भी कई तरह के होते हैं। तीन मुख्य ज्यामिति वाले संधारित्रों के बारे में नीचे की सारणी में मुख्य जानकारियाँ दी गयीं हैं। संधारित्र के दो चालकों (प्लेटों) के बीच के कुचालक की एक मुख्य गुण उसकी परमिटिविटी (permitivity) है जो ε से निरूपित की जाती है। निर्वात की परमिटिविटी को ε₀ से निरुपित किया जाता है। इसका मान है:

$\varepsilon_0=8{,}8542\cdot 10^{-12}\;\mathrm{F/m}$.

प्रकार	धारिता	विद्युत क्षेत्र	चित्र
समान्तर प्लेट संधारित्र	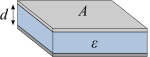$C = \varepsilon_0\varepsilon_\mathrm{r} \cdot \frac{A}{d}$	$E = \frac{Q}{\varepsilon_0 \varepsilon_\mathrm{r} A}$
बेलनाकार संधारित्र	$C=2\pi \varepsilon_0\varepsilon_\mathrm{r} \, \frac{l}{\ln\!\left(\frac{R_2}{R_1}\right)}$	$E(r) = \frac{Q}{2\pi r l \varepsilon_0 \varepsilon_\mathrm{r}}$
गोलीय संधारित्र	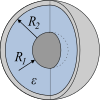$C=4 \pi \varepsilon_0 \varepsilon_\mathrm{r} \left( \frac{1}{R_1}-\frac{1}{R_2}\right)^{-1}$	$E(r) = \frac{Q}{4\pi r^2 \varepsilon_0 \varepsilon_\mathrm{r}}$
गेंद	$C = 4 \pi \varepsilon_0 \varepsilon_\mathrm{r} R_1$
समान्तर बेलन (लेकर-लाइन Lecher lines)	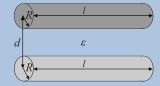$C = \frac{\pi \varepsilon l}{\rm arcosh\left(\frac {d}{2R}\right)}$
समतल प्लेट के समान्तर बेलन	$C = \frac{2\pi \varepsilon l}{\operatorname{arcosh}\left( \frac{d}{R}\right) }$		d > R
a त्रिज्या वाले दो गोले	$C = 2\pi \varepsilon a\left\{ \ln 2+\gamma -\frac{1}{2}\ln \left( \frac{d}{a}-2\right) +O\left( \frac{d}{a}-2\right) \right\}$

विभिन्न प्रकार के संधारित्र

आकार-प्रकार एवं गुणों में संधारित्र कई तरह के होते हैं।

मुख्य लेख : विभिन्न प्रकार के संधारित्र

इन्हें भी देखें

• परावैद्युत
• वैद्युत अवयव
• प्रतिरोधक
• प्रेरकत्व
• प्रत्यावर्ती धारा
• विद्युत परिपथ

बाहरी कड़ियाँ

• कैपेसिटर संग्राहक
• Capacitance and Inductance - a chapter from an online textbook
• Howstuffworks.com: How Capacitors Work
• CapSite 2009: Introduction to Capacitors
• Capacitor Tutorial - Includes how to read capacitor temperature codes
• Capacitor Converters and Calculators