मुक्त ज्ञानकोश विकिपीडिया से
गणित में लजान्द्र अवकल समीकरण का हल लजान्द्र बहुपद कहलाता है। लजान्द्र अवकल समीकरण निम्नोक्त है:
d
d
x
[
(
1
−
x
2
)
d
d
x
P
n
(
x
)
]
+
n
(
n
+
1
)
P
n
(
x
)
=
0.
{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}
यह नाम फ्रान्स के प्रसिद्ध गणितज्ञ आद्रियें मारि लजान्द्र के नाम पर पड़ा है । यह अवकल समीकरण भौतिकी एवं प्रौद्योगिकी में बार-बार देखने को मिलता है। विशेष रूप से, लाप्लास समीकरण को गोलीय निर्देशांक में हल करते समय यह समीकरण प्राप्त होता है।
लजान्द्र बहुपद, बहुपदों का एक सम्पूर्ण एवं आर्थोगोनल प्रणाली है। इनके अनेक गुण हैं और अनेकानेक उपयोग हैं।
n
P
n
(
x
)
{\displaystyle P_{n}(x)\,}
0
1
{\displaystyle 1\,}
1
x
{\displaystyle x\,}
2
1
2
(
3
x
2
−
1
)
{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(3x^{2}-1)\,}
3
1
2
(
5
x
3
−
3
x
)
{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(5x^{3}-3x)\,}
4
1
8
(
35
x
4
−
30
x
2
+
3
)
{\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(35x^{4}-30x^{2}+3)\,}
5
1
8
(
63
x
5
−
70
x
3
+
15
x
)
{\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(63x^{5}-70x^{3}+15x)\,}
6
1
16
(
231
x
6
−
315
x
4
+
105
x
2
−
5
)
{\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(231x^{6}-315x^{4}+105x^{2}-5)\,}
7
1
16
(
429
x
7
−
693
x
5
+
315
x
3
−
35
x
)
{\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(429x^{7}-693x^{5}+315x^{3}-35x)\,}
8
1
128
(
6435
x
8
−
12012
x
6
+
6930
x
4
−
1260
x
2
+
35
)
{\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)\,}
9
1
128
(
12155
x
9
−
25740
x
7
+
18018
x
5
−
4620
x
3
+
315
x
)
{\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)\,}
10
1
256
(
46189
x
10
−
109395
x
8
+
90090
x
6
−
30030
x
4
+
3465
x
2
−
63
)
{\displaystyle {\begin{matrix}{\frac {1}{256}}\end{matrix}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)\,}
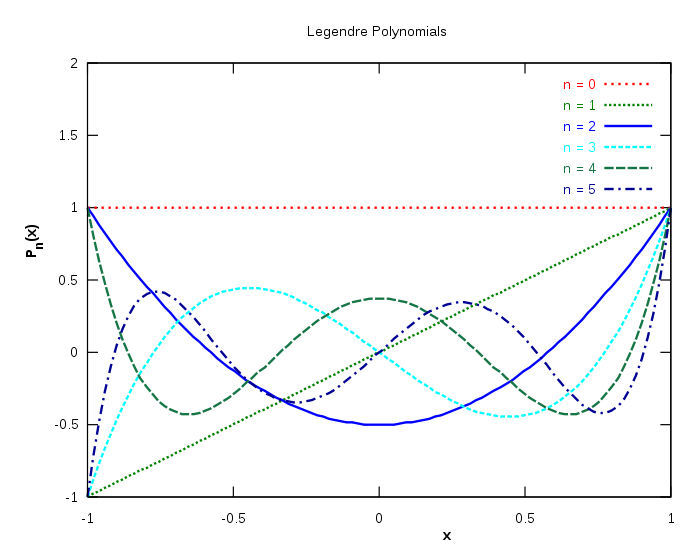
इन बहुपदों का ग्राफ नीचे दिखाया गया है (केवल n =5 तक) :

![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd51c7228067db4bea119843fb19c6caab834954)











