मुक्त ज्ञानकोश विकिपीडिया से
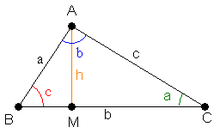
एक त्रिभुज जिसकी भुजाएँ a, b तथा c हैं। ज्यामिति में हीरोन का सूत्र त्रिभुज की तीनों भुजाएँ ज्ञात होने पर उसका क्षेत्रफल निकालने का एक सूत्र है। इसे हीरो का सूत्र भी कहते हैं। सूत्र का यह नाम अलेक्ज़ैंड्रिया के हीरोन के नाम पर पड़ा है।
इस सूत्र के अनुसार, यदि किसी त्रिभुज की तीन भुजाएँ a, b और c हों तो उसका क्षेत्रफल
A
=
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
{\displaystyle A={\sqrt {s(s-a)(s-b)(s-c)}}}
जहाँ s उस त्रिभुज का अर्धपरिमाप है, अर्थात्
s
=
a
+
b
+
c
2
{\displaystyle s={\frac {a+b+c}{2}}}
हीरोन का सूत्र चक्रीय चतुर्भुज का क्षेत्रफल निकालने के लिए ब्रह्मगुप्त के सूत्र की एक विशेष स्थिति (केस) है। ब्रह्मगुप्त का सूत्र यह है:
A
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
{\displaystyle A={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}
जहाँ,
s
=
a
+
b
+
c
+
d
2
{\displaystyle s={\frac {a+b+c+d}{2}}}
एक त्रिभुज की भुजाएँ 3, 4 तथा 5 हैं।
इसका अर्धपरिमाप
s
=
a
+
b
+
c
2
=
3
+
4
+
5
2
=
6
{\displaystyle s={\frac {a+b+c}{2}}={\frac {3+4+5}{2}}=6}
इसका क्षेत्रफल:
A
=
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
=
6
⋅
(
6
−
3
)
⋅
(
6
−
4
)
⋅
(
6
−
5
)
=
6
⋅
3
⋅
2
⋅
1
=
36
=
6.
{\displaystyle {\begin{aligned}A&={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}={\sqrt {6\cdot (6-3)\cdot (6-4)\cdot (6-5)}}\\&={\sqrt {6\cdot 3\cdot 2\cdot 1}}={\sqrt {36}}=6.\end{aligned}}}
पार्श्व चित्र में
b
{\displaystyle b}
h
{\displaystyle h}
A
=
b
h
2
.
{\displaystyle A={\frac {bh}{2}}.}
कोज्या सूत्र के अनुसार,
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
=
a
2
+
b
2
−
2
b
a
2
−
h
2
,
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C=a^{2}+b^{2}-2b{\sqrt {a^{2}-h^{2}}},}
अतः
h
2
=
a
2
−
(
a
2
+
b
2
−
c
2
2
b
)
2
.
{\displaystyle h^{2}=a^{2}-\left({\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)^{2}.}
अतः
A
2
=
b
2
h
2
4
=
b
2
(
a
2
−
(
a
2
+
b
2
−
c
2
2
b
)
2
)
4
=
(
2
a
b
)
2
−
(
a
2
+
b
2
−
c
2
)
2
16
=
(
2
a
b
−
(
a
2
+
b
2
−
c
2
)
)
(
2
a
b
+
(
a
2
+
b
2
−
c
2
)
)
16
=
=
(
c
2
−
(
a
−
b
)
2
)
(
(
a
+
b
)
2
−
c
2
)
16
=
(
c
−
a
+
b
)
(
c
+
a
−
b
)
(
a
+
b
−
c
)
(
a
+
b
+
c
)
16
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
s
{\displaystyle {\begin{matrix}A^{2}&=&{\frac {b^{2}h^{2}}{4}}={\frac {b^{2}\left(a^{2}-\left({\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)^{2}\right)}{4}}={\frac {(2ab)^{2}-(a^{2}+b^{2}-c^{2})^{2}}{16}}={\frac {(2ab-(a^{2}+b^{2}-c^{2}))(2ab+(a^{2}+b^{2}-c^{2}))}{16}}=\\\\&=&{\frac {(c^{2}-(a-b)^{2})((a+b)^{2}-c^{2})}{16}}={\frac {(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{16}}=(s-a)(s-b)(s-c)s\\\end{matrix}}}