प्रसामान्य बंटन

प्रसामान्य बंटन
Normal distribution

इनमें लाल वक्र 'मानक प्रसामान्य बंटन' है।
Cumulative distribution function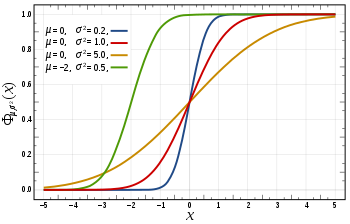
Notation	${\mathcal {N}}(\mu ,\,\sigma ^{2})$
Parameters	μ ∈ R — mean (location) σ2 > 0 — variance (squared scale)
Support	x ∈ R
	${\frac {1}{\sqrt {2\sigma ^{2}\pi }}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$
CDF	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$
Quantile	$\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2F-1)$
Mean	μ
Median	μ
Mode	μ
	$\sigma ^{2}\,$
Skewness	0
Ex. kurtosis	0
Entropy	${\tfrac {1}{2}}\ln(2\sigma ^{2}\pi \,e\,)$
MGF	$\exp\{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}\}$
CF	$\exp\{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}\}$
Fisher information	${\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$

प्रायिकता सिद्धान्त में प्रसामान्य बंटन या गाउसीय बंटन (normal distribution या Gaussian distribution) वह सतत प्रायिकता बंटन है जो प्रकृति में सामान्यतः पाया जाता है। प्रसामान्य बंतन सांख्यिकी में महत्वपूर्ण है। प्राकृतिक विज्ञानों और सामाजिक विज्ञानों में इनका उपयोग वास्तविक मान वाले यादृच्छिक चरों को निरुपित करने के लिये किया जाता है।

प्रसामान्य बंटन का प्रायिकता घनत्व निम्नलिखित होता है-

$f(x\;|\;\mu ,\sigma ^{2})={\frac {1}{\sqrt {2\sigma ^{2}\pi }}}\;e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$

जहाँ:

• $\mu$ बंटन का माध्य या अपेक्षित मान है (यह बटन का मध्य (median) तथा बहुलक (mode) भी होता है)
• $\sigma$ मानक विचलन है,
• $\sigma ^{2}$ प्रसरण है।

किसी यादृच्छिक चर का बंटन प्रसामान्य बंटन हो तो उसे प्रसामान्य बंटित चर कहते हैं।

प्रसामान्य संभाव्यता वक्र

नॉर्मल प्रोबेबिलिटी कर्व एनपीसी प्रसामान्य संभाव्यता वक्र अन्य वितरण आंकड़ों के आधार पर तैयार होता है जिसे या प्रसामान्य वितरण वक्र एनपीसी कहां जाता है दूसरे शब्दों में प्रसामान्य पत्र से तात्पर्य होता है जिसके द्वारा प्रसामान्य वितरण नॉर्मल डिस्ट्रीब्यूशन का प्रतिनिधित्व होता है अर्थ वैसे वितरण से होता है जिसमें बहुत सारे के मापनी मैं आते ही तथा बहुत कम कैसे मापनी की ऊपरी चोर तथा बहुत कम केसेस मापनी के निचले छोर पर आते हैं इस तरह के वितरण से बनने को घंटाघर बकरा या बॉल सेव कर कहां जाता है अन्य नामो जैसे फ्रूट कार ऑफ एयर डिनो वर्ष वक्र गौ सीमन बकरा ही कहा जाता है जैसे अगर किसी कक्षा के विद्यार्थियों की बुद्धि लब्धि निकाली जाए तो बहुत उम्मीद है कि आप क्योंकि बुद्धि लब्धि 110 के बीच आएगी खुद ही कम विद्यार्थियों की बुद्धि लब्धि 70-80 मापनी के निचले छोर तथा 130 - 140 मापनी के ऊपर छोड़कर भीतर आएगी इस तरह के वितरण को हम प्रसामान्य वितरण कहेंगे और इससे जो वक्त बनेगा उसे प्रसामान्य वक्र कहा जाता है हिंदी के आधार पर प्रसामान्य पत्र को घंटा कार्यक्रम आ जाता है क्योंकि इसकी आकृति घंटा की आकृति से बहुत कुछ मिलती जुलती है

प्रसामान्य वक्र की प्रमुख विशेषताएं

1.प्रसामान्य वक्र सममित समिट ट्रिकल होता है सममित होने से मतलब की प्रसामान्य वक्र के का हिस्सा हिस्से के बराबर होता है तुम्हें यह कहा जा सकता है कि प्रसामान्य वक्र का बाया भाग तथा दाया भाग बराबर होते हैं।

=2. प्रसामान्य वक्र मैं माध्य माध्यिका तथा बहुलक संख्यात्मक रूप से एक ही होते हैं तथा वक्र के ठीक बीचोबीच एक बिंदु केंद्रित होते हैं तथा क्रिकेट ठीक बीचोबीच एक बिंदु पर केंद्रित होता है।

=3. प्रसामान्य वक्र अनंतस्पर्शी स्थान पर आधार रेखा को स्पर्श नहीं करते|

=4.प्रसामान्य वक्र घंटा करता है जिसका कारण यह है कि ऐसे वक्र द्वारा वितरण का सबसे अधिक कैसे है होते हैं जैसे-जैसे इन मध्य से हम बाई तथा दाई तरफ बढ़ते हैं कैसे की संख्या में कमी आती जाती है।

=5. प्रसामान्य वक्र सतत होता है फलत x स्तर पर चरो के मान की संख्या अनिश्चित होती है।

=6. खड़ी रेखा की ऊंचाई भोज मान .3989 के बराबर होता है।

=7. प्रसामान्य वक्र में वक्र वक्र के कुल क्षेत्र का 68.2 6% माध्य -1 सिग्मा +1 सिग्मा की बीच होता है, इस वक्र के कुल क्षेत्र का 95% भाग - 1.96व +1.96 सिग्मा के मध्य होता है तथा 99% मान ±2.58 सिग्मा के मध्य होता है।

सन्दर्भ

पूनम मॉथम(m.ed)