ऊष्मागतिकी का प्रथम नियम
उष्मागतिकी के शून्यवें सिद्धांत में ताप की भावना का समावेश होता है। यांत्रिकी में, विद्युत् या चुंबक विज्ञान में अथवा पारमाण्वीय विज्ञान में, ताप की भावना की कोई आवश्यकता प्रतीत नहीं होती है । उष्मागतिकी के प्रथम सिद्धांत द्वारा ऊष्मा की भावना का समावेश होता है। जूल के प्रयोग द्वारा यह सिद्ध होता है कि किसी भी पिंड को (चाहे वह ठोस हो या द्रव या गैस) यदि स्थिरोष्म दीवारों से घेरकर रखें तो उस पिंड को एक निश्चित प्रारंभिक अवस्था से एक निश्चित अंतिम अवस्था तक पहुँचाने के लिए हमें सर्वदा एक निश्चित मात्रा में कार्य करना पड़ता है। कार्य की मात्रा पिंड की प्रारंभिक तथा अंतिम अवस्थाओं पर ही निर्भर रहती है, इस बात पर नहीं कि यह कार्य कैसे किया जाता है। यदि प्रारंभिक अवस्था में दाब तथा आयतन के मान p0 तथा V0 हैं तो कार्य की मात्रा अंतिम अवस्था की दाब तथा आयतन पर निर्भर रहती है, अर्थात् कार्य की मात्रा p तथा V का एक फलन है। यदि कार्य की मात्रा का W हैं तो हम लिख सकते हैं कि
W = U - U0 (4)
यह समीकरण एक राशि U की परिभाषा है जो केवल उस पिंड की अवस्था पर ही निर्भर रहती है न कि इस बात पर कि वह पिंड उस अवस्था में किस प्रकार पहुँचा है। इस राशि को हम पिंड की आंतरिक ऊर्जा कहते हैं। यदि कोई पिंड एक निश्चित अवस्था से प्रारंभ करके विभिन्न अवस्थाओं में होते हुए फिर उसी प्रारंभिक अवस्था में आ जाए तो उसकी आंतारिक ऊर्जा में कोई अंतर नहीं होगा, अर्थात्
f dU = 0 (5)
और (dU) एक यथार्थ अवकल (परफ़ेक्ट डिफ़रेन्शियल) है।
यदि कोई पिंड एक अवस्था से दूसरी अवस्था में जाए तो (U-U0-W) का मान सर्वदा शून्य के बराबर नहीं होगा। यदि प्रत्येक अवस्था के लिए U का मान ज्ञात कर लिया गया है तो यह अंतर ज्ञात किया जा सकता है। यदि पिंड की दीवारों का कोई भाग उष्मागम्य है तो सर्वदा इस अंतर के बराबर ऊष्मा उस पिंड को देनी पड़ेगी। यदि ऊष्मा की मात्रा Q है तो
Q = U - U0 - W (6)
इस समीकरण में Q उन्हीं एककों में नापा जाएगा जिसमें W, परंतु यदि हमने Q का एकक पहले ही निश्चित कर लिया है तो हम इस समीकरण द्वारा इन दोनों एककों का अनुपात ज्ञात कर सकते हैं। इस प्रकार जूल के प्रयोग द्वारा हम ऊष्मा का यांत्रिक तुल्यांक निकाल सकते हैं। इस प्रयोग में Q शून्य के बराबर होता है और (U-U0) का मान ऊष्मा के एककों में ज्ञात किया जाता है।
समीकरण (6) उष्मागतिकी के प्रथम सिद्धांत का गणितीय रूप है। इसमें W वह कार्य है जो बाहर से उस पिंड पर किया जाता है। यदि यह पिंड स्वयं कार्य करे, जिसका परिणाम dW हो और किसी प्रक्रम (प्रोसेस) में निकाय की आंतरिक ऊर्जा जिस परिमाण में बढ़े वह dU हो तो गिनती ऊष्मा उस निकाय को दी जाएगी वह तो dQ होगी और
dQ = dU + dW (7)
और आगे बढ़ने के पहले हम एक ऐसे प्रक्रम का वर्णन करेंगे जिसका उपयोग उषमागतिकी में बहुत किया जाता है। इसे प्राय: स्थैतिक (सिस्टम) के आयतन को एक अत्यणु परिमाण dV से परिवर्तित करें तो इसका ताप भी थोड़ा परिवर्तित हो जाएगा। साम्यावस्था प्राप्त होने पर इसके आयतन में मान ले हम थोड़ा और अत्यणु परिवर्तित करें। इस तरह हम धीरे धीरे अवस्था 1 से अवस्था 2 में पहुँच जायँगे। यदि हमारे परिवर्तनों का परिमाण धीरे-धीरे शून्य की ओर बढ़े तो अंत में 1 से 2 तक परिवर्तन कहते हैं। ऐसे प्रक्रम का यह भी लक्षण है कि विस्थापनों, किए गए कार्य एवं अवशोषित ऊष्मा के चिह्नों को उलटकर इस निकाय को अवस्था 2 से कारण इन प्रक्रमों को उत्क्रमणीय प्रक्रम कहते हैं। जो प्रक्रम उत्क्रमणीय नहीं होते उन्हें अनुत्क्रमणीय प्रक्रम कहते हैं।
यह सरलता से सिद्ध किया जा सकता है कि यदि किसी निकाय की दाब p हो तो एक उत्क्रमणीय प्रक्रम में यह जो कार्य करेगा वह pdV के बराबर होगा। अतएव उष्मागतिकी के प्रथम सिद्धांत को हम इस तरह भी लिख सकते हैं :
dQ = dU + pdV (8)
विशेष स्थितियाँ[संपादित करें]
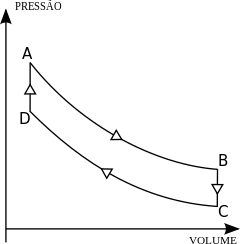
ऊष्मागतिकी के प्रथम नियम के समीकरण में आने वाले चरों के मान, कुछ विशेष स्थितियों में, नीचे दिए गये हैं-
| रुद्धोष्म | , = - |
| नियत आयतन V | , = |
| चक्रीय | , |
| स्वतंत्र प्रसार | , |








