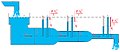
बर्नौली का प्रमेय

तरल के दो बिन्दुओं पर स्तर में अंतर ऊपर वेन्च्युरी नली में हवा के बहाव में अंतर के अनुपात में और उसके कारण है। यही बर्नौली के सिद्धान्त से भी सिद्ध होता है।

तरल गतिकी में, बर्नौली का सिद्धान्त (Bernoulli's principle) या 'बर्नौली का प्रमेय निम्नवत है:

किसी प्रवाह में, तरल का वेग बढ़ने पर पर तरल की स्थितिज उर्जा में कमी होती है या उस स्थान पर दाब में कमी हो जाती है। यह सिद्धान्त डच-स्विस गणितज्ञ डैनियल बर्नौली के नाम पर रखा गया है। इस सिद्धान्त की खोज उन्होंने ही की थी और १७३८ में अपनी 'हाइड्रोडाय्नैमिका' नामक पुस्तक में प्रकाशित किया था।

बर्नौली समीकरण का विशेष स्थिति में स्वरूप

माना कि:

• तरल असंपीड्य (इन्कम्प्रेसिबल) है,
• श्यानता शून्य है,
• स्थाई अवस्था प्राप्त हो गयी है तथा प्रवाह अघूर्णी िर्रोटेशनल) है, तो

इस स्थिति में बर्नौली का समीकरण निम्नवत है:

${e_m} = {v^2 \over 2}+gh+{p \over \varrho}=\mathrm{const}$

जहाँ:

• $\; e_m \;$ - तरल के ईकाई द्रव्यमान की ऊर्जा
• $\; \varrho \;$ - तरल का घनत्व
• $\; v \;$ - संबन्धित स्थान पर तरल का वेग
• $\; h \;$ - सम्बन्धित स्थान की किसी सन्दर्भ के सापेक्ष ऊँचाई
• $\; g \;$ - गुरुत्वजनित त्वरण
• $\; p \;$ - संबन्धित स्थान पर दाब

बाहरी कड़ियाँ

• Interactive animation demonstrating Bernoulli's principle
• Denver University – Bernoulli's equation and pressure measurement
• Millersville University – Applications of Euler's equation
• NASA – Beginner's guide to aerodynamics
• Misinterpretations of Bernoulli's equation – Weltner and Ingelman-Sundberg
• Video demonstration of levitating ping pong ball