किरचॉफ के परिपथ के नियम

सन् १८४५ में गुस्ताव किरचॉफ (या, गुस्ताव किरखॉफ) ने विद्युत परिपथों में वोल्टता एवं धारा सम्बन्धी दो नियम प्रतिपादित किये। ये दोनो नियम संयुक्त रूप से किरचॉफ के परिपथ के नियम कहलाते हैं। ये नियम विद्युत परिपथों के लिये वस्तुतः आवेश संरक्षण एवं उर्जा संरक्षण के नियमों के भिन्न रूप हैं। ये नियम वैद्युत इंजीनियरी से सम्बन्धित गणनाओं के आधार हैं और बहुतायत में प्रयोग होते हैं। ये दोनो नियम मैक्सवेल के समीकरणों से सीधे व्युत्पन्न किये जा सकते हैं किन्तु इतिहास यह है कि किरचॉफ ने इन्हें मैक्सवेल से पहले प्रतिपादित कर दिया था।
किरचॉफ का धारा का नियम (केसीएल / KCL)

i1 + i4 = i2 + i3
इस नियम को 'किरचॉफ का संधि नियम', 'किरचॉफ का बिन्दु नियम', 'किरचॉफ का जंक्सन का नियम' और किरचॉफ का प्रथम नियम भी कहते हैं।[1]
n किसी नोड से जुड़ी धारा-शाखाओं की कुल संख्या है।
यह नियम समिश्र धाराओं के लिये भी सत्य है।
यह नियम आवेश के संरक्षण के नियम पर आधारित है।
किरचॉफ का विभवान्तर का नियम (केवीएल / KVL)
v1 + v2 + v3 + v4 = 0
इस नियम को 'किरचॉफ का द्वितीय नियम', किरचॉफ का लूप (या मेश) का नियम भी कहते हैं।[2]
- T किसी घेरा (लूप) के परित: सभी विभवान्तरों का बीजगणितीय योग शून्य होता है।
अर्थात,
यहाँ, n लूप में स्थित कुछ विभवान्तरों की संख्या के बराबर है। ये विभवान्तर समिश्र संख्या (जैसे एसी विश्लेषण की स्थिति में) भी हो सकते हैं।
यह नियम उर्जा संरक्षण के नियम पर आधारित है।
उदाहरण

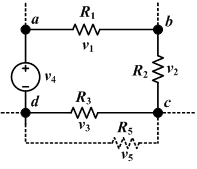
सामने दिखाये गये विद्युत परिपथ में 2 वोल्टता स्रोत तथा 3 प्रतिरोधक हैं। तथा,
किरचॉफ के प्रथम नियम के अनुसार हम लिख सकते हैं कि
अब बन्द परिपथ (लूप) s1 में किरचॉफ के द्वितीय नियम के अनुसार,
इसी तरह बन्द परिपथ s1 में किरचॉफ के द्वितीय नियम के अनुसार,
इस प्रकार हमें में निम्नलिखित रैखिक समीकरण प्राप्त हुए-
इनको सरल करके इस प्रकार भी लिख सकते हैं-
अब
रखने पर निम्नलिखित हल प्राप्त होता है-
ध्यान दीजिये कि का चिह्न ऋणात्मक है, जिसका मतलब यह है कि वास्तव में की दिशा चित्र में दिखायी गयी दिशा के उल्टी दिशा में है।
इन्हें भी देखें
बाहरी कड़ियाँ
- http://www.sasked.gov.sk.ca/docs/physics/u3c13phy.html[मृत कड़ियाँ]
- MIT video lecture on the KVL and KCL methods
- किरचॉफ का नियम आसानी से समझे।
सन्दर्भ
- ↑ "किरचौफ के धारा नियम". मूल से 3 अप्रैल 2010 को पुरालेखित. अभिगमन तिथि 2 अप्रैल 2010.
- ↑ "किरचौफ के विभव नियम". मूल से 2 अप्रैल 2010 को पुरालेखित. अभिगमन तिथि 2 अप्रैल 2010.














![{\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}\\[6pt]i_{2}={\frac {4}{275}}\\[6pt]i_{3}=-{\frac {3}{220}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/566ea3f52c6f5f749bdf9c861ac42e960f5b8919)
