विवर्तन

एक वर्गाकार द्वारक (aperture) से विवर्तन के परिणामस्वरूप पर्दे पर निर्मित विवर्तन पैटर्न

जब प्रकाश व ध्वनि तरंगे किसी अवरोध से टकराती हैं, तो वे अवरोध के किनारों पर मुड जाती हैं और अवरोधक की ज्यामितिय छाया में प्रवेश कर जाती हैं। तरंगो के इस प्रकार मुड़ने की घटना को विवर्तन (Diffraction) कहते हैं। ऐसा पाया गया है कि लघु आकार के अवरोधों से टकराने के बाद तरंगें मुड़ जातीं हैं तथा जब लघु आकार के छिद्रों (openings) से होकर तरंग गुजरती है तो यह फैल जाती है। सभी प्रकार की तरंगों से विवर्तन होता है (ध्वनि, जल तरंग, विद्युतचुम्बकीय तरंग आदि)।

परिचय एवं इतिहास

यदि किसी प्रकाशोत्पादक स्रोत और पर्दे के बीच कोई अपारदर्शक वस्तु रख दी जाए, तो पर्दे पर वस्तु की छाया बन जाती है। बहुधा छाया का किनारा तीक्ष्ण (sharp) होता है और उसके चारों ओर पर्दे का भाग समान रूप से प्रकाशित रहता है। यदि प्रकाशोत्पादक स्रोत बिंदुवत् छोटा हो, तो ध्यान से देखने पर छाया का किनारा तीक्ष्ण नहीं पाया जाता है। किनारे पर प्रकाश और अंधकार (brightness and darkness) की धारियाँ दिखाई पड़ती हैं। ऐसा मालूम होता है कि प्रकाश की किरणें मुड़कर ज्यामितीय छाया की सीमा के भीतर तक पहुंच गई हैं। इस घटना को प्रकाश का विवर्तन कहते हैं। छाया के किनारे-किनारे जो धारियाँ बनती हैं, उन्हें विवर्तन पैटर्न (Diffraction Pattern) कहा जाता है। विवर्तन की जानकारी से पूर्व यही माना जाता था कि किसी एक माध्यम में प्रकाश सीधी रेखाओं में चलता है। किंतु विवर्तन की व्याख्या प्रकाश के सरल रैखिक गमन के आधार पर नहीं की जा सकती है। सर्वप्रथम न्यूटन (Newton), ग्रिमाल्डी (Grimaldi) और टी. यंग (T. Young) ने इस घटना पर ध्यान दिया था। न्यूटन और ग्रिमाल्डी प्रकाश के कणिका सिद्धांत (Corpuscular Theory) के प्रवर्तक और अनुयायी थे, अत: उन्होंने विवर्तन की घटना को इसी आधार पर समझने का असफल प्रयास किया। बाद में क्रिश्चियन हाइगेंज ने प्रकाश के तरंग सिद्धांत का प्रतिपादन किया और ए. जे. फ्रेनेल (A. J. Fresnel) तथा फ्राउनहोफर (Fraunhofer) ने इसी सिद्धांत के आधार पर विवर्तन तथा विवर्तन से संबंधित अन्य घटनाओं को सफलता पूर्वक समझाया।

जब प्रकाश के मार्ग में गोल छेद, आयताकार रेखाछिद्र, किसी वस्तु की तीक्ष्ण कोर (edge) या महीन तार रखा जाता है, तब प्रत्येक दशा में भिन्न प्रकार के विवर्तन पैटर्न बनते हैं। विवर्तन की सभी घटनाओं को दो विभागों में बाँटा जा सकता है :

• (1) फ्राउनहोफर विवर्तन (Fraunhofer Diffraction), और
• (2) फ्रेनेल विवर्तन (Fresnel Diffraction)।

जब प्रकाशस्रोत और पर्दा विवर्तक वस्तु से अत्यंत दूर होते हैं, अर्थात् विवर्तक पर समतल तरंगाग्र (plane wavefront) अपातित होता है, तब विवर्तन पैटर्न को फ्राउनहोफर पैटर्न और घटना को फ्राउनहोफर विवर्तन कहा जाता है। जब स्रोत, पर्दा, या ये दोनों, विवर्तक वस्तु से नियत (finite) दूरी पर होते हैं, अर्थात् विवर्तक पर गोलीय या बेलनाकार तरंगाग्र आपतित होता है, तब विवर्तन की घटना को फ्रेनेल विवर्तन कहा जाता है। फ्रेनेल विवर्तन देखना अपेक्षाकृत सरल होता है, किंतु इसे समझना कठिन होता है। फ्राउनहोफर विवर्तन देखने के लिए विशेष प्रकार की व्यवस्था करनी पड़ती है, जिससे समतल तरंगाग्र प्राप्त हो। विवर्तन के बाद उसे पुन: फोकस करने की व्यवस्था करनी पड़ती है, किंतु इसका सिद्धांत समझना बहुत सरल है।

फ्राउनहोफर विवर्तन:- ऐसा विवर्तन जिसमें प्रकाश स्रोत तथा पर्दा अवरोधक से अनन्त दूरी पर हो।

अकेले रेखाछिद्र का विवर्तन पैटर्न (Diffraction pattern of single slit)

सोडियम लैम्प से पीले रंग का एकवर्णी प्रकाश (monochromatic light) प्राप्त होता है। एक लेंस की सहायता से इस प्रकाश को एक काले पर्दे में कटे हुए अत्यंत सँकरे रेखाछिद्र (slit) पर डाला जाए, तो यही रेखाछिद्र स्वयं एक प्रकाश स्रोत का काम देता है। अब इस रेखाछिद्र के आगे लेंस लगाकर समांतर किरणपुंज को एक दूसरे रेखाछिद्र पर डाला जाए तथा इस रेखाछिद्र के पीछे सफेद पर्दा रखा जाए, तो पर्दें पर दूसरे रेखाछिद्र का विवर्तन पैटर्न बन जाता है। इस पैटर्न के बीच में अत्यंत तीव्र बैंड (intense band) या पट्टी होती है। इस पट्टी के दोनों ओर अपेक्षाकृत बहुत कम तीव्रता की और भी पट्टियाँ पाई जाती हैं। बीचवाली पट्टी को मुख्य उच्चिष्ठ (Principal Maxima) तथा अन्य पट्टियों को द्वितीयक उच्चिष्ठ (Secondary Maxima) कहते हैं।

विवर्तन ग्रेटिंग (Diffraction Grating)

दो समीपवर्ती रेखाछिद्रों का विवर्तन पैटर्न एक रेखाछिद्र के विवर्तन पैटर्न से कुछ भिन्न होता है। एक रेखाछिद्र के पैटर्न में जहाँ जहाँ उच्चिष्ठ मिलता है, दो रेखाछिद्र के पैटर्न में उन्हीं स्थानों पर कई धारियाँ बनती हैं, जो पहले के बैंडों की अपेक्षा अधिक पतली और तीक्ष्ण होती हैं। ज्यों-ज्यों रेखाछिद्रों की संख्या बढ़ती जाती है, द्वितीयक उच्चिष्ठ की धारियाँ क्षीण होती जाती हैं और मुख्य उच्चिष्ठ की धारियाँ अत्यंत तीक्ष्ण होती जाती हैं। रेखाछिद्रों की चौड़ाई तथा उनकी पारस्परिक दूरी भी इन धारियों की तीक्ष्णता को बहुत प्रभावित करती है। शीशे की समतल पट्टी पर हीरे की कनी से रेखाएँ खींच दी जाएँ, तो प्रत्येक दो रेखा के बीच का पारदर्शक स्थान रेखाछिद्र का काम करता है। ऐसे ही रेखाछिद्रों के समूह को ग्रेंटिंग कहते हैं। ग्रेटिंग का आविष्कार फ्राउनहोफर ने किया था। उन्होंने दो स्क्रू के ऊपर महीन तार लपेटकर ग्रेटिंग बनाया था। प्रत्येक दो तारों के बीच का स्थान रेखाछिद्र का काम करता है। आगे चलकर उन्होंने काँच के प्लेट पर रेखाएँ खींचकर ग्रेटिंग बनाया। रोलैंड ने 1882 ई. में ग्रेटिंग की रेखाएँ बनानेवाली मशीन बनाई। आजकल अच्छी मशीनों द्वारा एक इंच पर 30,000 या 40,000 तक रेखाएँ खींची जाती हैं।

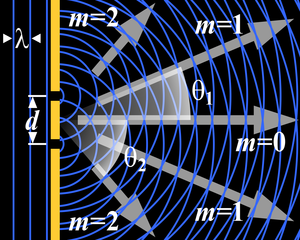
यदि किसी प्रकाशस्रोत के सम्मुख लेंस रखकर, एकवर्णी समांतर किरणों को एक ग्रेटिंग पर डाला जाए, तो इससे प्राप्त विवर्तन में एक दूसरी से दूर दूर कई तीक्ष्ण रेखाएँ पाई जाती हैं। ये रेखाएँ वास्तव में रेखाछिद्र स्रोत का विवर्तन बिंब होती हैं। बीच की सबसे तीव्र रेखा को शून्य कोटि (Zero order) की रेखा कहते हैं। इसके दोनों ओर पहली, दूसरी, तीसरी आदि रेखाएँ क्रमश: प्रथम, द्वितीय तथा तृतीय कोटि की रेखाएँ कहलाती हैं। यदि ग्रेटिंग पर श्वेत प्रकाश डाला जाए, तो शून्य कोटि की रेखा श्वेत होती है, किंतु अन्य कोटि की रेखाओं स्थान पर स्पेक्ट्रम प्राप्त होते हैं। इन्हें क्रमश: प्रथम, द्वितीय, तृतीय आदि कोटि के स्पेक्ट्रम कहा जाता है। यदि ग्रेटिंग से विवर्तित होनेवाले प्रकाश का तरंगदैर्घ्य l, आपतित तरंगाग्र का आपतन कोण i और विवर्तन कोण q हो तथा किन्हीं दो समीपस्थ रेखाछिद्रों के मध्यबिंदुओं की पारस्परिक दूरी d हो, तो

d (sin-i + sin q) = n l होता है। n स्पेक्ट्रम की कोटि (order) का द्योतक है।

ऊपर जिस ग्रेटिंग का विवरण दिया गया है, उसे समतल विवर्तन ग्रेटिंग कहते हैं। यदि वक्र शीशे पर ऐलुमिनियम की कलई कर दी जाए और उसी पर हीरे की कनी से रेखाएँ खुरच दी जाएँ, तो प्रत्येक दो रेखाओं के बीच का भाग एक नन्हें परावर्ती दर्पण का काम करता है। इन भागों से परावर्तित तरंगों के व्यतिकरण से भी विवर्तन पैटर्न बनता है। इस ग्रेटिंग को अवतल ग्रेटिंग (Concave grating) कहते हैं। इसका आविष्कार रोलैंड (Rowland) ने किया था। अवतल ग्रेटिंग अवतल दर्पण का भी काम करता है। अत: विवर्तित किरणों को फोक्स करने के लिए लेंस का प्रयोग नहीं करना पड़ता है।

स्पेक्ट्रमिकी (spectroscopy) में स्पेक्ट्रम प्राप्त करने के लिए वक्र ग्रेटिंग से बड़े उपयोगी स्पेक्ट्रोग्राफ बनाए गए हैं। वक्र ग्रेटिंग के लिए भी तरंगदैर्घ्य का सूत्र d (sin i + sin q) = n l ही होता है। दो विभिन्न वर्णों की रश्मियों (l1, l2) को एक दूसरे से पृथक् करने की क्षमता को ग्रेटिंग की वर्णविक्षेपण क्षमता (Dispersive Power) कहा जाता है। यदि l1- l2 = Dl हो और इनके विवर्तन कोण क्रमश: q1 और q2 हों तथा q1 - q2 = Dq हो, तो ग्रेटिंग की वर्ण विक्षेपण क्षमता होती है। तरंगदैर्घ्य के सूत्र से इसका मान होता है। क्रमश: उच्चतर कोटि में वर्ण विक्षेपण क्षमता बढ़ती जाती है। यदि l और l+dl दो अत्यंत समीपवर्ती विकिरण (radiations) हों और ग्रेटिंग द्वारा इनको एक दूसरे से अलग-अलग देखा जा सके तो dl को ग्रेटिंग की विभेदन क्षमता (resolving power) कहते हैं। N ग्रेटिंग पर बनी हुई कुल रेखाओं (या रेखाछिद्रों) की संख्या है। क्रमश: उच्च्तर कोटि में विभेदन क्षमता भी बढ़ती जाती है।

फ्रेनेल विवर्तन

फ्रैनेल विवर्तन :-एसा विवर्तन जिस में प्रकाश स्रोत तथा पर्दा अवरोधक या द्वारक से सीमीत दूरी पर हो।

छाया का बनना

छाया के किनारे पर विवर्तन पैटर्न का बनना प्रकाश के सरल रैखिक गमन से नहीं समझाया जा सकता है। इसे समझाने के लिए फ्रैनेल ने तरंग सिद्धांत का उपयोग किया। किसी तरंगाग्र के विभिन्न बिंदुओं का प्रभाव समझाने के लिए उन्होंने अर्ध काल जोन (Half Period Zones) का सिद्धांत प्रतिपादित किया। इस सिद्धांत के आधार पर बनाया गया ज़ोन प्लेट लेंस की भाँति काम करता है और फ्रेनेल के सिद्धांत की पुष्टि करता है।

गोल छिद्र से विवर्तन

यदि किसी अत्यंत छोटे छिद्र पर एकवर्णी समतल तरंगाग्र आपतित होता हो, तो पर्दें पर इसका विवर्तन पैटर्न बन जाता है। इस पैटर्न में वृत्ताकार धारियाँ (circular fringes) पाई जाती हैं। सबसे बाहरी धारी सबसे अधिक मोटी होती है और भीतरी धारियाँ क्रमश: पतली होती हैं। फ्रेनेल के अर्धकाल ज़ोन के आधार पर इस विवर्तन की व्याख्या की जा सकती है।

यदि छिद्र का आकार प्रथम अर्धकाल ज़ोन के बराबर हो और पैटर्न के केंद्र तथा छिद्र की परिधि की दूरियों का अंतर (2m+1) l/2 हो, तो पैटर्न का केंद्र प्रकाशित होता है। यदि पर्दे से छिद्र की दूरी स्थिर रखकर छिद्र का आकार बढ़ाते जाएँ, तो यह केंद्र क्रमश: प्रकाशित (bright) और अप्रकाशित (dark) होता है। जब छिद्र का आकार (2m+1) अर्धकाल-ज़ोन समाविष्ट करता है, तो पैटर्न का केंद्र चमकीला होता है और जब छिद्र में 2m अर्ध-काल-ज़ोन समाविष्ट होते हैं, तो केंद्र काला होता है। छिद्र को स्थिर रखकर पर्दें को उससे समीप या दूर लाने पर भी केंद्र पर परिवर्तन होता है। यदि पैटर्न के केंद्र से छिद्र के केंद्र और छिद्र की परिधि की दूरियों का अंतर (2 m+1) l/2 हो, तो केंद्र चमकीला, अन्यथा काला, होता है।

गोल डिस्क के विवर्तन पैटर्न के केंद्र पर सर्वदा एक चमकीली बिंदी बनती है।

प्रकाशीय यंत्रों की विभेदन क्षमता (Resolving power of optical instruments)

किसी प्रकाशीय यंत्र द्वारा किसी बिंदु स्रोत का बिंब (image) वास्तव में उस यंत्र के द्वारक (aperture) से होकर जानेवाली तरंगों का विवर्तन पैटर्न होता है। यदि दो बिंदु स्रोत अत्यंत पास पास हों, तो यंत्र द्वारा प्रत्येक का एक-एक विवर्तन पैटर्न बनता है। चूँकि सभी प्रकाशीय यंत्रों में वर्तुल द्वारक (circular aperture) होता है, अत: बिंदु स्रोतों के विवर्तन पैटर्न में वर्तुल बिंदु (spot) बनता है और उसके किनारे किनारे कई वर्तुल वलय (rings) होते हैं। यंत्र का द्वारक जितना ही बड़ा होता है, विवर्तन पैटर्न उतने ही छोटे बनते हैं। यदि प्रकाशीय यंत्र द्वारा दो अत्यंत समीपस्थ बिंदु स्रोतों के विवर्तन पैटर्न इतने छोटे और स्पष्ट बनें कि एक का केंद्रीय महत्तम (central maximum) प्रकाशित भाग दूसरे के सर्वप्रथम न्यूनतम (first minimum) प्रकाशित भाग पर पड़े, तो दोनों के केंद्रीय बिंदु (spots) स्पष्ट देखें जा सकते हैं। प्रकाशीय यंत्र की इस क्षमता को विभेदन क्षमता (Resolving Power) कहते हैं।

किरीट या कोरोना (Corona)

बहुधा आकाश में बादलों की उपस्थिति के समय सूर्य अथवा चंद्रमा के चारों ओर एक चमकीला घेरा दिखाई पड़ता है। इसे किरीट कहते हैं। पानी की नन्हीं बूँदों द्वारा प्रकाश का विवर्तन होने से ही किरीट बनते हैं। स्पष्ट किरीट के लिए नन्हीं बूँदों का समाकार होना आवश्यक होता है। ये बूँदे जितनी ही अधिक छोटी होती हैं किरीट का व्यास उतना ही बड़ा होता है। टी यंग (T. Young) ने किरीटों का व्यास नापकर जलकणों के व्यास की गणना करने के लिए यंत्र बनाया था, जिसे तंतुमापी (Eriometer) कहते हैं।

विवर्तन और व्यतिकरण में भेद

विवर्तन और व्यतिकरण में सिद्धांतत: कोई भेद नहीं है। तब भी बहुधा यह कहा जाता है कि व्यतिकरण में कुछ नियत संख्या के प्रकाशपुंजों का अध्यारोपण (superposition) होने से तरंग आयाम (wave amplitude) के प्रत्येक अतिसूक्ष्म खण्डों (elements) के प्रभाव का समाकलन (integrate) करके तरंग का आयाम ज्ञात किया जाता है। एक से अधिक रेखाछिद्रों का विवर्तन पैटर्न, विवर्तन और व्यतिकरण के संयुक्त प्रभाव से, बनता है। संक्षेप में; विवर्तन, व्यतिकरण का ही किंचित् क्लिष्ट रूप है।

बाहरी कड़ियाँ

• Do Sensors “Outresolve” Lenses?; on lens and sensor resolution interaction.
• Diffraction and acoustics.
• Diffraction in photography.
• On Diffraction at MathPages.
• Diffraction pattern calculators at The Wolfram Demonstrations Project
• Wave Optics – A chapter of an online textbook.
• 2-D wave Java applet – Displays diffraction patterns of various slit configurations.
• Diffraction Java applet – Displays diffraction patterns of various 2-D apertures.
• Diffraction approximations illustrated – MIT site that illustrates the various approximations in diffraction and intuitively explains the Fraunhofer regime from the perspective of linear system theory.
• Gap Obstacle Corner – Java simulation of diffraction of water wave.
• Google Maps – Satellite image of Panama Canal entry ocean wave diffraction.