मुक्त ज्ञानकोश विकिपीडिया से
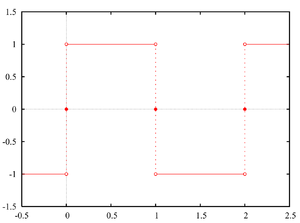
वर्ग तरंगरूप (square wave) वह आवर्ती तरंग है जिसका मान हर T/2 समय बाद +h से -h में क्रमशः बदलता रहता है। वस्तुतः यह एक गैर-ज्यावक्रीय तरंगरूप (non-sinusoidal waveform) है। व्यवहार में ऐसी तरंग प्राप्त करना सम्भव नहीं है, क्योंकि शून्य समय में अधिकतम से न्यूनतम मान में बदलता किसी भौतिक प्रणाली में सम्भव नहीं है।
यदि किसी वर्ग तरंग की उँचाई h हो तथा उसकी मूल आवृत्ति f हो तो उस तरंग का फुर्ये विश्लेषण करने पर निम्नलिखित प्रकार से अभिव्यक्त कर सकते हैं-
f
(
t
)
=
4
h
π
[
sin
(
ω
t
)
+
1
3
sin
(
3
ω
t
)
+
1
5
sin
(
5
ω
t
)
+
…
]
{\displaystyle f(t)={\frac {4h}{\pi }}\left[\sin(\omega t)+{\frac {1}{3}}\sin(3\omega t)+{\frac {1}{5}}\sin(5\omega t)+\ldots \right]}
=
4
h
π
∑
k
=
1
∞
sin
(
(
2
k
−
1
)
ω
t
)
2
k
−
1
{\displaystyle ={\frac {4h}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin((2k-1)\omega t)}{2k-1}}}
जहाँ
ω
=
2
π
f
{\displaystyle \omega =2\pi f}
किसी 1000 Hz की वर्ग तरंग में उपस्थित सन्नादी (हार्मोनिक्स) । ध्यान दें कि इसमें केवल विषम सन्नादी ही हैं, सभी सम सन्नादियों का मान शून्य है। वर्ग तरंग को अन्य गणितीय रूपों में भी अभिव्यक्त किया जा सकता है, जैसे-
(1)
x
(
t
)
=
sgn
(
sin
(
t
)
)
{\displaystyle \ x(t)=\operatorname {sgn}(\sin(t))}
(2) वर्ग तरंग को हेविसाइड स्टेप फलन u (t ) के माध्यम से या आयताकार फलन (rectangular function) Π(t ) के माध्यम से भी अभिव्यक्त किया जा सकता है:
x
(
t
)
=
2
[
∑
n
=
−
∞
∞
Π
(
2
(
t
−
n
T
)
T
−
1
2
)
]
−
1
=
2
∑
n
=
−
∞
∞
[
u
(
t
T
−
n
)
−
u
(
t
T
−
n
−
1
2
)
]
−
1.
{\displaystyle {\begin{aligned}x(t)&=2\left[\sum _{n=-\infty }^{\infty }\Pi \left({\frac {2(t-nT)}{T}}-{\frac {1}{2}}\right)\right]-1\\&=2\sum _{n=-\infty }^{\infty }\left[u\left({\frac {t}{T}}-n\right)-u\left({\frac {t}{T}}-n-{\frac {1}{2}}\right)\right]-1.\end{aligned}}}
(3)
x
(
t
)
=
{
1
,
0
<
t
≤
T
0
,
T
<
t
≤
2
T
{\displaystyle \ x(t)={\begin{cases}1,&0<t\leq T\\0,&T<t\leq {2T}\end{cases}}}
तथा
x
(
t
+
T
)
=
x
(
t
)
{\displaystyle \ x(t+T)=x(t)}


![{\displaystyle f(t)={\frac {4h}{\pi }}\left[\sin(\omega t)+{\frac {1}{3}}\sin(3\omega t)+{\frac {1}{5}}\sin(5\omega t)+\ldots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be83823e1567f78352ec587329eed4d3be4d18d3)



![{\displaystyle {\begin{aligned}x(t)&=2\left[\sum _{n=-\infty }^{\infty }\Pi \left({\frac {2(t-nT)}{T}}-{\frac {1}{2}}\right)\right]-1\\&=2\sum _{n=-\infty }^{\infty }\left[u\left({\frac {t}{T}}-n\right)-u\left({\frac {t}{T}}-n-{\frac {1}{2}}\right)\right]-1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64023feb7c2635877ec4a5e073e8ab92e0223396)

