फ्लिप-फ्लॉप
| यह लेख एक आधार है। जानकारी जोड़कर इसे बढ़ाने में विकिपीडिया की मदद करें। |


एलेक्ट्रॉनिकी में द्विमानित्र (फ्लिप-फ्लॉप) एक अंकीय (डिजिटल) परिपथ है जिसका निर्गम (आउटपुट) दो स्थाई अवस्थाओं में से किसी एक में बना रहता है (जब तक उसे बदलने के लिये निवेश (इनपुट) में कुछ न किया जाय)। इसे 'लैच' (latch) भी कहते हैं। इस परिपथ में एक या एक से अधिक निवेश होते हैं जिन पर संकेत का उचित परिवर्तन करके निर्गम के अवस्था (स्टेट) को बदला जा सकता है। इसके एक एक या दो निर्गम होते हैं।
द्विमानित्र कई प्रकार के होते हैं और आंकिक एलेक्ट्रॉनिकी की मूलभूत निर्माण-ईकाई हैं। ये आंकड़ा भंडारण के अवयव (अर्थात 'मेमोरी') तैयार करने के लिये प्रयुक्त होते हैं। ये 'अनुक्रमिक तर्क' (sequential logic) की श्रेणी में आते हैं। इनका उपयोग स्पंदों (पल्सों) को गिनने (काउन्टर) के लिये तथा अलग-अलग समय पर पहुंचने वाले निवेश संकेतों को समकालिक बनाने (synchronizing) के लिये किया जाता है।
इतिहास[संपादित करें]
प्रथम द्विमानित्र (फ्लिप-फ्लॉप) परिपथ का आविष्कार सन १९१८ में हुआ था जो निर्वात नली का उपयोग करके बनाया गया था। उस समय उसका नाम 'एक्लीज-जॉर्डन ट्रिगर परिपथ' (Eccles–Jordan trigger circuit) था। बाद में ट्रांजिस्टर से द्विमानित्र बने और आजकल एकीकृत परिपथ के रूप में उपलब्ध हैं।
प्रकार[संपादित करें]
- सेट-रिसेट लैच या एस-आर लैच (बिना गेट वाले 'सरल' लैच तथा गेटेड एस-आर द्विमानित्र)
- डी द्विमानित्र
- टी द्विमानित्र
- जेके द्विमानित्र
टी फ्लिप-फ्लॉप[संपादित करें]
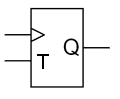
Q* → Q के बाद की अवस्था
सिंक्रोनस RS फ्लिप-फ्लॉप[संपादित करें]


J-K फ्लिप-फ्लाप[संपादित करें]


D (Data) फ्लिप-फ्लॉप[संपादित करें]
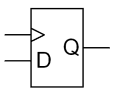
प्रमुख द्विमानित्र (फ्लिप-फ्लॉप) की अवस्था-परिवर्तन सारणी[संपादित करें]
संकेत:
- X - यह 1 या 0 कुछ भी हो,
- Qt - पिछली अवस्था (स्टेट),
- Qt+1 - वर्तमान अवस्था।
| Qt | Qt+1 | D | T | SR | JK |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0X | 0X |
| 0 | 1 | 1 | 1 | 10 | 1X |
| 1 | 0 | 0 | 1 | 01 | X1 |
| 1 | 1 | 1 | 0 | X0 | X0 |

