शांकव

शांकवों के विभिन्न रूप

शांकवों की सूची, साइक्लोपीडिया, 1728

गणित में, किसी लम्ब वृत्तीय शंकु की एक समतल द्वारा परिच्छेद करने से प्राप्त वक्रों (curves) को शांकव (conicsection) कहते हैं।
शांकव की एक अन्य परिभाषा के अनुसार शांकव(समतल मे) किसी एसे चर बिन्दु का बिन्दुपथ है जिसकी एक निर्धारित बिन्दु एवं एक निर्धारित रेखा से दूरियोँ का अनुपात हमेशा स्थिर(अच‍र) रहता है। इस परिभाषा का प्रयोग कर किसी भी निर्देशांक पद्धति‎ मे शांकव को एक गणितीय समीकरण के रूप मे प्राप्त कर सकते हैं

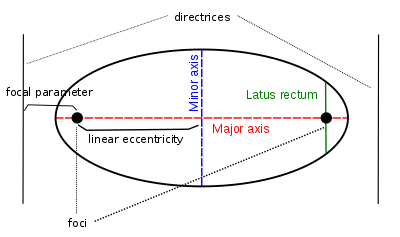
शांकव के अवयव [संपादित करें]

यदि कोई बिंदु इस प्रकार से गमन करता है कि उसकी एक स्थिर बिंदु से दुरी तथा उसकी एक स्थिर सरल रेखा से दुरी का अनुपात सदैव एक अचर संख्या (Costant) हो,तो उस बिंदु के बिन्दुपथ को एक शंकु परिच्छेद कहते हैं ।

नाभि
शांकव कि परिभाषा मे प्रयुक्त एक निश्चित बिन्दु शांकव की नाभि(फोकस) कहलाता है।
नियता
शांकव कि परिभाषा मे प्रयुक्त एक निश्चित रेखा शांकव की नियता कहलाती है।
उत्केन्द्रता
शांकव कि परिभाषा मे प्रयोग किया गया निश्चित अनुपात ही को उत्केन्द्रता कह्ते हैं। इसे e से दर्शाते हैं।

e = (चर बिन्दु की नाभि से दूरी) / (चर बिन्दु की नियता से दूरी)

अक्ष
शांकव की नियता के लंबवत व नाभि (फोकस) से जाने वालि रेखा अक्ष होती है'
शीर्ष
शांकव की अक्ष जिस बिन्दु पर वक्र को काटती है वह बिन्दु,
शीर्ष पर स्पर्शी
शांकव अक्ष के लंबवत शीर्ष से जाने वाली स्पर्श रेखा,

शांकवों के विभिन्न रूप [संपादित करें]

समतल और लम्ब वृत्तीय शंकु का परिच्छेद से प्राप्त वक्र का स्वरूप इस बात पर निर्भर करता है कि समतल, शंकु को किस प्रकार काटता है।

शांकव के अंतर्गत निम्नलिखित वक्र आते हैं:

वृत्त (circle) : $e=0$
दीर्घवृत्त (ellipse) : $0<e<1$
परवलय (parabola) : $e=1$
अति परवलय (hyperbola) : $e>1$
रेखा-युग्म (pair of straight lines)

एक नियत नाभि (फोकस) एवं डाइरेट्रिक्स के वाले दीर्घवृत्त (e=1/2), परवलय (e=1) एवं अतिपरवलय (e=2)

दीर्घवृत्त की Semi-latus rectum

विशेषताएँ [संपादित करें]

शांकव	समीकरण	उत्केंद्रता (e)	रैखिक उत्केंद्रता (c)	semi-latus rectum (ℓ)	focal parameter (p)
वृत्त	$x^2+y^2=a^2 \,$	$0 \,$	$0 \,$	$a \,$	$\infty$
दीर्घवृत्त	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$	$\sqrt{1-\frac{b^2}{a^2}}$	$\sqrt{a^2-b^2}$	$\frac{b^2}{a}$	$\frac{b^2}{\sqrt{a^2-b^2}}$
परवलय	$y^2=4ax \,$	$1 \,$	$a \,$	$2a \,$	$2a \,$
अतिपरवलय	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	$\sqrt{1+\frac{b^2}{a^2}}$	$\sqrt{a^2+b^2}$	$\frac{b^2}{a}$	$\frac{b^2}{\sqrt{a^2+b^2}}$