कृष्णिका

भौतिक विज्ञान में कृष्णिका पदार्थ की एक आदर्शीकृत अवस्था है, जो अपने ऊपर पड़ने वाले सभी विद्युत चुम्बकीय विकिरण अवशोषित कर लेता है। एक ऐसी वस्तु जो अपने पृष्ठ पर आपतित सभी तरंगदैध्यो के विकिरणो का पूर्णतयः अवशोषण कर लेती है उसे कृष्णिका कहते है। कृष्णिका एक विशेष और सतत वर्णक्रम (स्पेक्ट्रम) में विकिरण को अवशोषित और गर्म होने पर फिर से उत्सर्जित करते हैं। क्योंकि कोई भी प्रकाश (दृश्य विद्युत चुम्बकीय विकिरण) परिलक्षित या संचरित नहीं होता है और वस्तु जब ठंडी होती है, तो काली दिखाई देती है। हालांकि एक कृष्णिका तापमान पर निर्भर प्रकाश वर्णक्रम का उत्सर्जन करता है। कृष्णिका से निकले इस सौर विकिरण को कृष्णिका विकिरण कहा जाता है। कृष्णिका के वर्णक्रम में तरंग की लंबाई (तरंगदैर्घ्य) जितनी छोटी होती है, आवृत्ति उतनी ही ज्यादा होती है और उच्च आवृत्ति उच्च तापमान से संबंधित होती है। इस प्रकार, एक गर्म वस्तु का रंग वर्णक्रम के नीले अंत के करीब होता है और एक ठंडी वस्तु का रंग लाल के करीब होता है।
कमरे के तापमान पर, कृष्णिका ज्यादातर अवरक्त (इंफ्रारेड) तरंगदैर्घ्य फेंकते हैं, लेकिन तापमान के कुछ सौ डिग्री सेल्सियस बढ़ जाने पर कृष्णिका दृश्य तरंगदैर्घ्य उत्सर्जित करते हैं, जो तापमान बढ़ने के साथ ही लाल, नारंगी, पीले, उजले, नीले दिखते हैं। वस्तु के सफेद होने तक वह पर्याप्त मात्रा में पराबैंगनी विकिरण उत्सर्जित करती है। "कृष्णिका" शब्द 1860 मेंगुस्ताव किर्चाफ के द्वारा शुरू किया गया। जब इसका यौगिक विशेषण के रूप में प्रयोग किया जाता है, तो यह शब्द आम तौर पर "कृष्णिका विकिरण" या " ब्लैकबॉडी रेडियेशन" के रूप में एक शब्द में संयुक्त हो जाता है।
कृष्णिका उत्सर्जन एक निरंतर जारी रहने वाले क्षेत्र के सौर संतुलनस्थिति की अंतर्दृष्टि प्रदान करता है। शास्त्रीय भौतिकी में सौर संतुलन में प्रत्येक अलग-अलग फूरियर मोड में समान ऊर्जा होनी चाहिए। इस दृष्टिकोण से एक विरोधाभास पैदा हुआ, जिसे पराबैंगनी आपदा के रूप में जाना जाता है और जिसमें सतत जारी रहने वाले क्षेत्र में ऊर्जा की एक अपार मात्रा होती है। कृष्णिका सौर संतुलन के गुणों का परीक्षण कर सकते हैं, क्योंकि वे जो सूर्य की किरणों द्वारा वितरित किये जाने वाले विकिरण उत्सर्जित करते हैं। ऐतिहासिक रूप से कृष्णिका के नियमों का अध्ययन करने से ही क्वांटम यांत्रिकी की अवधारणा आई।
व्याख्या[संपादित करें]

कृष्णिका का विकिरण एक खास तापमान में कृष्णिका के साथ सौर संतुलन और प्रकाश विकिरण का प्रकाश होता है। यह प्रकाश के थर्मोडायनेमिक्स (उष्मगतिकी) संतुलन की स्थिति को सन्दर्भित करता है। प्रयोगात्मक रूप से यह कृष्णिका युक्त एक कठोर-दीवारों वाली गुहा में स्थिर स्थिति संतुलन विकिरण के रूप में स्थापित हो चुका है। प्रकृति में दृढ़ता से कोई वास्तविक कृष्णिका नहीं होते लेकिन ग्रेफाइट एक अच्छा सादृश्य है और स्थिर स्थिति पर ग्रेफाइट दीवारों युक्त एक बंद बॉक्स कृष्णिका के आदर्श विकिरण का एक अच्छा सन्निकटन है।[1][2][3] एक गुहा, जिसमें कोई कृष्णिका नहीं है, वह संतुलन की स्थिति में कृष्णिका विकिरण बरकरार रखने में सक्षम नहीं है, यह तथ्य किर्चाफ द्वारा प्रयोगात्मक रूप से पाया गया है, लेकिन इसका भौतिक महत्व न तो किर्चाफ ने समझा और न ही प्लैंक ने.
चूंकि प्रकाश निरंतरविद्युत चुम्बकीय क्षेत्र का एक दोलायमान रूप है, कृष्णिका के विकिरण-अध्ययन से पता चलता है कि सतत क्षेत्रों में कैसा तापमान होता है, जो शास्त्रीय भौतिकी से विरोधाभास प्रकट करता है। क्योंकि क्वांटम यांत्रिकी के आगमन से पहले प्रकाश की सौर स्थिति इतनी भ्रमित करने वाली थी कि 19 वीं सदी के इन तर्कों को काफी सावधानी से पेश किया गया कि प्रकाश की एक सौर संतुलन स्थिति होती है।
निर्धारित तापमान में टी में कोई पदार्थ एक ओवन की तरह चमकता हुआ देखा जा सकता है। जिस बिंदु पर सभी ठोस पदार्थ एक मंद लाल चमक (करीब 798 के) पैदा करते हैं, उस बिंदु को ड्रेपर बिंदु नाम दिया गया।[4][5] 1000 के पर एक ओवन लाल दिखता है और 6000 के पर यह सफेद दिखाई देता है। जब तक ओवन काफी चमकदार नहीं होता तब तक इससे कोई अंतर नहीं पड़ता है कि भट्ठी का निर्माण कैसे किया गया है, प्रकाश का रंग केवल तापमान पर निर्भर करता है। चूंकि रंग तरंगदैर्घ्य का प्रत्यक्ष रूप से दर्शनीय उपाय है, इसलिए यह कहने का मतलब है कि अलग-अलग तापमान पर प्रकाश से अलग-अलग तरंगदैर्घ्य के बीच भिन्न-भिन्न ऊर्जा वितरित होती है। टी तापमान पर λ तरंगदैर्घ्य में प्रति यूनिट वोल्युम ई ऊर्जा की मात्रा को कृष्णिका घुमाव की अवस्था कहा जाता है। विस्तृत प्रयोगों से पता चला है कि कृष्णिका के घुमाव की अवस्था केवल तापमान पर निर्भर करती है, न कि उत्सर्जित पदार्थ पर. इससे यह पता चलता है कि किसी भी अन्य वस्तु की तरह प्रकाश वास्तव में सौर संतुलन से आता है और इस प्रकार टी तापमान में प्रकाश की अवधारणा समझ में आती है।

समान तापमान पर दो चीजें संतुलन में रह सकती हैं, जैसे टी तापमान पर प्रकाश के बादल से घिरा पदार्थ टी तापमान पर औसत रूप से बादल में उतना प्रकाश विकिरित कर सकता है, जितना वह सोख ले, यह प्रीवोस्ट के विनिमय सिद्धांत पर आधारित है, जो विकरणशील संतुलन को सन्दर्भित करता है। विस्तृत संतुलन का सिद्धांत कहता है कि उत्सर्जन और अवशोषण की प्रक्रिया के बीच कोई अजीब किस्म का सह-संबंध नहीं है, उत्सर्जन की प्रक्रिया अवशोषण से प्रभावित नहीं होती बल्कि यह केवल उत्सर्जन कर रहे पदार्थ की सौर स्थिति से प्रभावित होती है। इसका मतलब यह हुआ कि टी तापमान पर पदार्थ द्वारा उत्सर्जित कुल प्रकाश, चाहे वह कृष्ण पदार्थ हो या नही, हमेशा उस कुल प्रकाश के बराबर होता है, जिसे पदार्थ अवशोषित करता है, जो टी तापमान पर प्रकाश से घिरा हो।
कृष्णिका के लिए अवशोषित प्रकाश की मात्रा उतनी होती है, जितनी वह सतह पर पड़ती है। किसी भी तरंगदैर्घ्य λ के प्रति ईकाई समय में अवशोषित प्रकाश ऊर्जा अनिवार्य रूप से कृष्णिका के कर्व के अनुपात में होती है। इसका मतलब है कि कृष्णिका का घुमाव कृष्णिका द्वारा उत्सर्जित प्रकाश ऊर्जा जितना है, जो इसके नाम को उपयुक्त ठहराता है। यह सौर विकिरण का किरचॉफ नियम है: कृष्णिका का उत्सर्जन घुमाव प्रकाश की सौर विशेषता है, जो केवल गुहा की दीवारों केतापमानपर ही निर्भर करता है, बशर्ते यह स्थिति होनी आवश्यक है कि गुहा में कुछ पूरी तरह से काली सामग्री हो और यह विकरणशील संतुलन में हो। [6] जब कृष्णिका इतना छोटा हो कि इसके आकार की प्रकाश के तरंगदैर्घ्य से तुलना की जा सके तो अवशोषण संशोधित हो जाता है, क्योंकि एक छोटी सी वस्तु लंबे तरंगदैर्घ्य के प्रकाश का एक कुशल अवशोषक नहीं हो सकती, लेकिन उत्सर्जन और अवशोषण की कठोर समानता के सिद्धांत हमेशा सही ठहराये जाते हैं।
प्रयोगशाला में, कृष्णिका के विकिरण की मात्रा का अनुमान एक बड़ी गुहा के प्रवेशद्वार पर एक छोटे छेद, एकहोहलेरम, जिसमें कृष्णिका होता है और जिसे संतुलन तक पहुंचाया जाता है और बरकरार रखा जाता है, के जरिये लगाया जाता है। (यह तकनीक वैकल्पिक शब्द गुहा विकिरण की ओर ले जाती है). इस छेद में प्रवेश करने वाली प्रकाश की किसी किरण को निकलने से पहले गुहा की दीवारों पर कई बार प्रतिबिंबित होना होता है, जिस प्रक्रिया में इसका अवशोषित होना लगभग निश्चित हो जाता है। यह प्रवेश कर रहे विकिरण के तरंगदैर्घ्य से मतलब रखे बिना भी हो सकता है (जब तक कि यह छेद की तुलना में छोटा रहता है). तब यह छेद एक सैद्धांतिक कृष्णिका के करीबी सन्निकटन के रूप में होगा और यदि गुहा को गर्म किया जाये तो छेद के विकिरण का वर्णक्रम (जैसे प्रत्येक तरंगदैर्घ्य पर छेद से उत्सर्जित प्रकाश की राशि) सतत होगा, हालांकि यह भी पूरी सुनिश्चित करना होगा कि गुहा में लगभग पूरी तरह से काली कुछ सामग्री रखी गई हो और यह भी कि संतुलन कायम किया गया है और इसे बरकरार रखा गया है, लेकिन इन प्रावधानों के साथ, यह आगे गुहा की अन्य सामग्रियों पर आश्रित नहीं रहती है। (उत्सर्जन वर्णक्रम की तुलना में).
19 वीं सदी के उत्तरार्द्ध के दौरान सैद्धांतिक भौतिकी में कृष्णिका के घुमाव की गणना एक प्रमुख चुनौती थी। आखिर इस समस्या का हल 1901 में मैक्स प्लैंक द्वारा कृष्णिका विकिरण के प्लैंक नियम द्वारा किया गया।[7] थर्मोडायनेमिक्स और इलेक्ट्रोमैगनेटिज्म से तालमेल रखते हुए उनहोंने वायेन के विकिरण नियम (वायन के विस्थापन नियम के साथ भ्रमित नहीं होना) में बदलाव किये और एक संतोषजनक तरीके से प्रयोगात्मक डेटा के उपयुक्त एक गणितीय सूत्र पाया। अपने फार्मूले की भौतिक व्याख्या पाने के लिए तब प्लैंक ने यह माना कि गुहा में दोलन की ऊर्जा (यानी कुछ मात्रा के गुणज पूर्णांक) संतुलित हो गई है। आइंस्टीन ने इस विचार को आगे बढ़ाया और 1905 में ही फोटो इलेक्ट्रिक प्रभाव की व्याख्या करने के लिए प्रस्तावित विद्युत चुम्बकीय विकिरण के परिमाणीकरण का प्रस्ताव दिया। इन सैद्धांतिक प्रगतियों के परिणामस्वरूप अंततः क्वांटम इलेक्ट्रोडायनेमिक्स ने क्लासिकल इलेक्ट्रोमैगेटिज्म को खत्म कर दिया। आज, इन क्वांटा (प्रमात्रा सिद्धांत) को फोटॉनकहा जाता हैं और सोचा जा सकता है कि कृष्णिका की गुहा में फोटॉन्स की गैस हो सकती हैं। इसके अलावा, इसने क्वांटम प्रोबेबलिटी डिस्ट्रीब्यूशंस के विकास को दिशा दिखाई, जिसे फर्मी-डायरेक स्टेटिक्स और बोस-आइंस्टीन स्टेटिक्स कहा गया व इनमें से प्रत्येक कण विभिन्न वर्गों के लिए लागू होते हैं, जिनका क्लासिकल डिस्ट्रीब्यूशंस के बदले क्वांटम मैकेनिक्स में प्रयोग किया जाता है। फेरमियोन और बोसॉन भी देखें .
वह तरंगदैर्घ्य, जिस पर विकिरण सबसे मजबूत होता है, वायेन का विस्थापन नियम कहलाता है और प्रति यूनिट क्षेत्र में उत्सर्जित समग्र शक्ति स्टीफन बोल्ट्जमान नियम द्वारा दिया गया। अतः जैसे-जैसे तापमान बढ़ता है, चमक का रंग लाल से पीले और फिर सफ़ेद से नीले में परिवर्तित होता है। यहां तक कि चोटी पर पहुंचा तरंगदैर्घ्य पराबैगनी में प्रवेश करता है, तो नीले तरंगदैर्घ्य में पर्याप्त विकिरण का उत्सर्जित होना जारी रहता है, जिससे पदार्थ नीले रंग में दिखता रहता है। यह कभी भी अदृश्य नहीं होगा- वास्तव में, दृश्य प्रकाश का विकिरण तापमान के साथ एक गति से बढ़ता रहता है।[8]
चमक या पर्यवेक्षित तीव्रता दिशा का कार्य नहीं है। इसलिए एक कृष्णिका एक परिपूर्ण लाम्बर्टियन रेडियेटर होता है।
असली वस्तुएं कभी भी पूर्ण आदर्श काले पदार्थों की तरह व्यवहार नहीं करतीं और इसके बदले एक तय आवृत्ति पर उत्सर्जित विकिरण, हो सकने वाले एक आदर्श उत्सर्जन का एक अंश है। एक सामग्री का उत्सर्जन बताता है कि एक वास्तविक पदार्थ एक कृष्णिका की तुलना में कितनी अच्छी तरह ऊर्जा का विकिरण करता है। यह {0}उत्सर्जन{/0} कई कारकों, जैसे तापमान, उत्सर्जन की दिशा और तरंगदैर्घ्य पर निर्भर करता है। हालांकि, इंजीनियरिंग में यह मान विशिष्ट है कि एक सतह का वर्णक्रमीय उत्सर्जन और अवशोषण तरंगदैर्घ्य पर निर्भर नहीं करते हैं, इसलिए उत्सर्जन एक निरंतर प्रक्रिया है। इसे ग्रे बॉडी पूर्वानुमान के रूप में जाना जाता है।
गैर-काली सतहों से निपटने के क्रम में आदर्श काले-पदार्थ के व्यवहार का अपसरण ज्यामितीय संरचना और रासायनिक समिश्रण दोनों द्वारा निर्धारित होता हैं और यह भी तय होना चाहिए लगभग कृष्णिका का विकरणशील संतुलन वर्तमान हो। यह किचार्फ नियम के करीब हैं : उत्सर्जन अवशोषण के बराबर होता है, इसलिए जो वस्तु पड़ रहे समस्त प्रकाश को अवशोषित नहीं करती वह एक आदर्श कृष्णिका की तुलना में कम विकिरण उत्सर्जित करेगी।
खगोल विज्ञान में तारों जैसे पिंडों को अक्सर कृष्णिका माना जाता है, हालांकि यह एक कमजोर सन्निकटन है। एक लगभग पूर्ण कृष्णिका विकिरण वर्णक्रम ब्रह्मांडीय सूक्ष्म तरंग पृष्ठभूमि विकिरण द्वारा ही प्रदर्शित होता है। विकिरण का फैलाव काले छेद द्वारा उत्सर्जित एक काल्पनिक कृष्णिका विकिरण है।
हालांकि प्लैंक के फार्मूले में भविष्यवाणी की गई है कि एक कृष्णिका सभी आवृत्तियों पर ऊर्जा का विकिरण करेगा, हालांकि यह फार्मूला तभी लागू होगा, जब अनेक फोटोन्स को मापा जा रहा हो। उदाहरण के लिए, कमरे के तापमान (300 के) पर एक वर्गमीटर के सतह क्षेत्र में एक कृष्णिका प्रत्येक 41 सेकेंड पर एक फोटोन की औसत दर पर दृश्य रेंज (390-750 एनएम) पर एक फोटोन उत्सर्जित करेगा, इसका मतलब यह हुआ कि ज्यादातर व्यावहारिक प्रयोजनों में एक ऐसा कृष्णिका दृश्य परास में उत्सर्जन नहीं करेगा। [9]
कृष्णिका अनुकारी (सिमुलेटर)[संपादित करें]
हालांकि एक कृष्णिका एक सैद्धांतिक वस्तु है (यानी उत्सर्जनई = 1.0), अवरक्त विकिरण को स्रोत के सामान्य अनुप्रयोग एक कृष्णिका के रूप में परिभाषित करते हैं, जब वस्तु 1.0 के उत्सर्जन (आम तौर पर ई =0.99 या बेहतर) तक पहुंचती है। जब एक अवरक्त विकिरण का स्रोत 0.99 से कम हो तो इसे "ग्रे बॉडी" के रूप में सन्दर्भित किया जाता है।[10] कृष्णिका अनुकारी (सिमुलेटर) के अनुप्रयोगों में आम तौर पर अवरक्त प्रणालियों और अवरक्त संवेदक उपकरण का परीक्षण और अंशांकन शामिल होता हैं।
अति कृष्णिका ऐसा ही एक उदाहरण है, जो निकल-फास्फोरस मिश्र धातु से बनाया जाता है। अभी हाल ही में, जापानी वैज्ञानिकों की एक टीम ने कृष्णिका के बहुत करीब की एक सामग्री बनाई है, जो लम्बवत कोण पर एकल दीवार वाले कार्बन नैनोट्यूब्स पर आधारित है, जो वर्णक्रम सीमा में पराबैंगनी से अवरक्त परास के आपतित प्रकाश के 98% से 99% भाग को अवशोषित करती है।[11]
कृष्णिका समीकरण[संपादित करें]
कृष्णिका विकिरण का प्लैंक का नियम[संपादित करें]
प्लैंक का नियम कहता है कि कि
जहां
- आई वी टी{/0{0}डीवी I(ν,T) dν ऊर्जा की वह मात्रा है, जो प्रति इकाई सतह क्षेत्र प्रति इकाई समय और प्रति ईकाई ठोस कोण के मुताबिक वी (ν) और तापमान टी (T) पर कृष्णिका के बीच आवृत्ति रेंज में उत्सर्जित होती है।
- एच प्लैंक स्थिरांक है;
- सी निर्वात में एक प्रकाश की गति है;
- के बोल्ट्जमान निरंतरता है
- वी (ν) विद्युत चुम्बकीय विकिरण की आवृत्ति है और
- टी (T) केल्विंस में तापमान है
- वी (ν) विद्युत चुम्बकीय विकिरण की आवृत्ति है और
- के बोल्ट्जमान निरंतरता है
- सी निर्वात में एक प्रकाश की गति है;
- एच प्लैंक स्थिरांक है;
वायेन का विस्थापन नियम[संपादित करें]
वायेन का विस्थापन नियम दिखाता है कि किसी भी तापमान पर कृष्णिका का विकिरण किसी अन्य तापमान पर वर्णक्रम से किस तरह संबंधित है। अगर हमें एक तापमान पर वर्णक्रम के आकार का पता है तो हम किसी अन्य तापमान पर आकार की गणना कर सकते हैं।
वायेन के विस्थापन नियम का एक परिणाम यह है कि एक तरंगदैर्घ्य, जिस पर कृष्णिका द्वारा उत्पादित विकिरण की तीव्रता अधिकतम होती है,, यह केवल तापमान का कार्य है
जहां निरंतर बी (b), जो वायेन की विस्थापन निरंतरता के रूप में जाना है, बराबर होता है2.8977685(51)×१०−3 m K.
ध्यान रहे कि चोटी की तीव्रता को प्रति यूनिट तरंगदैर्घ्य या प्रति यूनिट आवृत्ति की तीव्रता के सन्दर्भ में व्यक्त किया जा सकता है। चोटी के तरंगदैर्घ्य के लिए उपरोक्त अभिव्यक्ति प्रति यूनिट तरंगदैर्घ्य तीव्रता को दर्शाता है; जबकि प्लैंक के नियम का उपरोक्त खंड प्रति इकाई आवृत्ति के सन्दर्भ में जाना जाता है। आवृत्ति, जिस पर प्रति इकाई ऊर्जा आवृत्ति अधिकतम होती है उसे
- .[12] सन्दर्भ में जाना जाता है।
स्टीफन-बोल्ट्जमान नियम[संपादित करें]
इस नियम में कहा गया है कि एक कृष्णिका के प्रति इकाई सतह क्षेत्र से उत्सर्जित ऊर्जा सीधे अपने पूर्ण तापमान के चौथाई ऊर्जा के अनुपात में होती है। अर्थात्
जहां j * प्रति यूनिट क्षेत्र में विकिर्ण कुल ऊर्जा होती है, टी (T) तापमान होता है (एक तापमान प्रणाली में निर्दिष्ट, जहां 0 पूर्ण रूप में शून्य होता है, जैसे केल्विन स्केल में) और σ = 5.67×१०−8 W m−2 K−4स्टीफन-बोल्ट्जमान निरंतरता होता है।
एक मानव शरीर द्वारा उत्सर्जित विकिरण[संपादित करें]
कृष्णिका नियम मनुष्यों पर भी लागू किया जा सकता है। उदाहरण के लिए, एक व्यक्ति की कुछ ऊर्जा विद्युत चुम्बकीय विकिरण के रूप में विकिर्ण हो जाती है, जिनमें से अधिकांश अवरक्त होती हैं।
शुद्ध विकिरण ऊर्जा उत्सर्जित ऊर्जा और अवशोषित ऊर्जा के बीच का अंतर होती है:
स्टीफन-बोल्ट्जमान नियम को लागू करना,
- .
एक वयस्क का कुल सतह क्षेत्र 2 m² होता है और त्वचा का मध्य तथा दूर-अवरक्तउत्सर्जन तथा कपड़ों का ज्यादातर हिस्सा एकबद्धता के करीब होता है, क्योंकि यह सबसे अधिक गैर-धातु सतह होता है।[13][14] त्वचा का तापमान 33 डिग्री सेल्सियस[15] होता है, लेकिन कपड़े सतह के तापमान को 28 डिग्री सेल्सियस कम कर देते हैं, जब की परिवेश का तापमान 20 डिग्री सेल्सियस होता है।[16] इसलिए, शुद्ध विकिरणशील उष्मा का नुकसान करीब निम्नांकित होता है
- .
एक दिन में विकिर्ण कुल ऊर्जा 9 MJ (मेगाजुलस), या 2000 किलो कैलोरी (भोजन कैलोरी) होती है। 40 साल के एक पुरुष की बेसलचयापचय दर करीब 35 किलो कैलोरी/(m2·h)[17] होती है, जो प्रतिदिन 1700 किलो कैलोरी के बराबर होती है और इसे 2 मी 2.क्षेत्र माना जा सकता है। हालांकि, ण्क सुस्त वयस्क की मध्यम चयापचय दर 50 से 70% होती है, जो उनके बेसल दर से अधिक होती है।[18]
संवहन और वाष्पीकरण सहित अन्य महत्वपूर्ण थर्मल नुकसान तंत्र भी होता है। संवहन नगण्य होता है क्योंकि नूसेल्ट संख्या एक्य से काफी ज्यादा होती है। वाष्पीकरण (पसीना) की जरूरत तभी होती है, जब तापमान की लगातार अवस्था को बरकरार रखने के लिए विकिरण और संवहन अपर्याप्त होते हैं। नि:शुल्क संवहन दर तुलनात्मक हैं, कम यद्यपि कुछ हद तक विकरणशील दर की तुलना में कम होते हैं।[19] इस प्रकार, विकिरण ठंडे व स्थिर हवा में दो तिहाई तापीय ऊर्जा के नुकसान के बराबर होता है। कई मान्यताओं की अनुमानित प्रकृति को देखते हुए इसे केवल एक मोटे अनुमान के रूप में लिया जा सकता है। परिवेशी वायु गति, बलात् संवहन पैदा करता है, या वाष्पीकरण एक थर्मल नुकसान तंत्र के रूप में विकिरण का तुलनात्मक महत्व कम कर देता है।
इसके अलावा, वायेन के नियम को मनुष्य पर लागू करने के समय पता चलता है कि एक व्यक्ति द्वारा उत्सर्जित प्रकाश तरंगदैर्घ्य शिखर है।
- .
यही कारण है कि मानव विषयों के लिए बनाये गये थर्मल इमेजिंग उपकरण 7000-14000 नैनोमीटर्स तरंगदैर्घ्य के प्रति अधिक संवेदनशील होते हैं।
एक ग्रह और इसके तारे के बीच तापमान संबंध[संपादित करें]
मोटे तौर पर एक ग्रह के तापमान का अनुमान लगाने के लिए काले-पदार्थ के नियम का प्रयोग किया गया है। सतह ग्रीनहाउस प्रभाव के कारण अधिक गर्म हो सकती है।[20]
कारक[संपादित करें]

एक ग्रह का तापमान कुछ कारकों पर निर्भर करता है:
- अनुवर्ती विकिरण (उदाहरण के लिए सूर्य से)
- उत्सर्जित विकिरण (उदाहरण के लिएपृथ्वी की अवरक्त चमक)
- एलबेडो प्रभाव (प्रकाश का एक अंश जिसे ग्रह परावर्तित करता है)
- ग्रीन हाउस प्रभाव (वातावरण वाले ग्रहों के लिए)
- एक ग्रह द्वारा खुद भीतर से ऊर्जा उत्पन्न करना (रेडियोधर्मी क्षय, ज्वारीय उष्मीकरण और ठंडा करने के लिए एडियेबैटिक संकुचन
आंतरिक ग्रहों के लिए, घटना और उत्सर्जित विकिरण का तापमान पर सबसे ज्यादा महत्वपूर्ण प्रभाव पड़ता है। यह व्युत्पादन मुख्य रूप से उसके साथ संबंधित है।
व्युत्पादन[संपादित करें]
स्टीफन-बोल्ट्जमान नियम सूर्य द्वारा उत्सर्जित कुल ऊर्जा (ऊर्जा/सेकेंड) देता है।

जहां
- स्टीफन-बोल्ट्जमान निरंतरता है।
- सूर्य की सतह का तापमान है और
- सूर्य की त्रिज्या है।
- सूर्य की सतह का तापमान है और
सूर्य सभी दिशाओं में समान रूप से ऊर्जा उत्सर्जित करता है। इस वजह से, पृथ्वी उसके केवल एक छोटे से अंश से ही गर्म हो जाती है। सूर्य की जो ऊर्जा पृथ्वी पर पड़ती है (सबसे शीर्ष वातावरण पर) वह है:
तो
- पृथ्वी की त्रिज्या है और
- खगोलीय इकाई है, सूर्य और पृथ्वी के बीच की दूरी.
उच्च तापमान के कारण, सूरज भारी मात्रा में पराबैंगनी और दृश्य आवृत्ति रेंज (यूवी-विज़) (UV-Vis) पर उत्सर्जन करता है। इस आवृत्ति श्रृंखला में, पृथ्वी इस ऊर्जा का एक अंश 1- परावर्तित करती है, जहां यूवी-विज़ (UV-Vis) रेंज में पृथ्वी का एलबेडो और परावर्तन है। दूसरे शब्दों में, पृथ्वी सूर्य के प्रकाश का एक अंश अवशोषित करती है और बाकी को परावर्तित कर देती है। पृथ्वी और इसके वातावरण द्वारा अवशोषित ऊर्जा इस प्रकार व्यक्त की जाती है:
यहां तक कि पृथ्वी एक गोलाकार क्षेत्र (\pi R^2) के रूप में ही अवशोषित करती है, यह क्षेत्र की सभी दिशाओं में समान रूप से उत्सर्जन करती है। यदि पृथ्वी एक परिपूर्ण कृष्णिका होती तो यह स्टेपहान-बोल्ट्जमान विधि के अनुसार उत्सर्जन करती.
जहां T_{E} पृथ्वी का तापमान होता है। पृथ्वी, चूंकि सूर्य की तुलना में काफी कम तापमान रख्रती है, ज्यादातर वर्णक्रम के केवल अवरक्त (IR) हिस्से को उत्सर्जित करती है। इस आवृत्ति रेंज में, यह उस विकिरण को उत्सर्जित करती है, जो एक कृष्णिका द्वारा आईआर रेंज में उत्सर्जित औसत उत्सर्जकता है। तो पृथ्वी और इसके वातावरण द्वारा उत्सर्जित ऊर्जा इस प्रकार है:
यह मानते हुए कि पृथ्वी उष्ण संतुलन में है, अवशोषित ऊर्जा अवश्य ही उत्सर्जित ऊर्जा के बराबर होनी आवश्यक है :
1-6 समीकरणों में सौर और पृथ्वी की शक्ति की स्थानापन्न अभिव्यक्ति और सरल रूप में इसे यूं कहा जा सकता है:
दूसरे शब्दों में, मान्यताओं के मुताबिक, पृथ्वी का तापमान केवल सूर्य, सूर्य की त्रिज्या, पृथ्वी और सूर्य के बीच दूरी, एलबीडो और पृथ्वी के आईआर उत्सर्जन के तापमान पर ही निर्भर करता है।
पृथ्वी का तापमान[संपादित करें]
अगर हम सूर्य और पृथ्वी के लिए मापित मूल्यों का स्थानापन्न निकालें:
अगर हम यूनिटी का औसत उत्सर्जन तय करें, हम गणना कर सकते हैं कि पृथ्वी का "प्रभावी तापमान" ऐसा होगा :
- T_E = 254.356 के या -18.8 डिग्री सेल्सियस.
पृथ्वी का यही तापमान होगा अगर यह ग्रीनहाउस प्रभाव की अनदेखी करते हुए और एक अपरिवर्तनीय एलबीडो की स्थिति में यह अवरक्त स्थिति में एक पूर्ण कृष्णिका के रूप में विकिर्ण होती है। वास्तव में पृथ्वी अवरक्त में लगभग एक पूर्ण कृष्णिका के रूप विकिर्ण होती है, जो अनुमानित तापमान को प्रभावी तापमान से कुछ ही डिग्री ज्यादा अधिक बढ़ायेगा. यदि हम अनुमान करना चाहें कि अगर कोई वातावरण नहीं हो तो पृथ्वी का तापमान क्या होगा, तो हमें एक अनुमान के अच्छे जरिये के रूप में एलबीडो और चांद के उत्सर्जन का ध्यान में रखना होगा। एलबीडो और चंद्रमा का उत्सर्जन क्रमशः करीब 0.1054 के[22] और 0,95[23] होता है, जिससे करीब 1.36 डिग्री सेल्सियस तापमान पैदा होने का अनुमान है।
पृथ्वी का औसत एलबिडो का अनुमान 0.3-0.4 रेंज के बीच भिन्न-भिन्न होता है, जिसके परिणामस्वरूप अलग-अलग अनुमानित प्रभावी तापमान दिखता है। अनुमान अक्सर तापमान, आकार और सूरज की दूरी के बजाय सौर निरंतरता (कुल आतपन शक्ति का घनत्व) पर आधारित होता है। उदाहरण के लिए, एलबीडो के लिए 0.4 का और 1400 W m−2) के एक आतपन के उपयोग के जरिये करीब 245 के प्रभावी तापमान प्राप्त किया जा सकता है।[24] इसी तरह एलबीडो 0.3 और सौर निरंतरता 1372 W m−2), का उपयोग कर कोई 255 के का प्रभावी तापमान प्राप्त कर सकता है।[25][26]
एक चलायमान कृष्णिका के लिए डॉपलर प्रभाव[संपादित करें]
डॉपलर प्रभाव एक अच्छी तरह ज्ञात तथ्य है, जो यह वर्णित करता है कि प्रकाश की आवृत्तियां तब किस तरह "स्थानांतरित" हो जाती हैं, जब एक प्रकाश स्रोत पर्यवेक्षक के सापेक्ष घूम रहा होता है। अगर एफ एक एकवर्णी प्रकाश के स्रोत की उत्सर्जित आवृत्ति है, तो यह एफ आवृत्ति पर तब दिखेगा जब वह पर्यवेक्षक के सापेक्ष घूम रहा हो।
जहां v पर्यवेक्षक के रेस्ट फ्रेम में वेग का स्रोत है, तो θ वेग सदिश और पर्यवेक्षक स्रोत दिशा के बीच का कोण है और सी प्रकाश की गति है।[27] यह पूरी तरह से सापेक्षकीय सूत्र है और वस्तुओं के विशेष मामलों में जो सीधे तौर पर (θ = π) की दिशा में आगे बढ़ रहे हों या पर्यवेक्षक से दूर (θ =0) हों और सी से गति बहुत कम हो, इसे आसान किया जा सकता है।
एक चलायमान कृष्णिका के वर्णक्रम की गणना करने के लिए, यह स्पष्ट लगता है कि कृष्णिका वर्णक्रम की प्रत्येक आवृत्ति के लिए यह सूत्र लागू होता है। हालांकि, साधारण रूप से इसके जैसी प्रत्येक आवृत्ति की स्केलिंग पर्याप्त नहीं है। हमें दिख रहे विवर के परिमित आकार का हिसाब रखना होता है, क्योंकि प्रकाश प्राप्त कर रहा ठोस कोण भी लोरेंट्ज के बदलाव से प्रभावित होता है। (हम बाद में विवर को मनमाने ढंग से छोटा होने की अनुमति दे सकते हैं और स्रोत को स्वच्छंदतापूर्वक दूर रख सकते हैं, लेकिन शुरू में इसे अनदेखा नहीं किया जा सकता.) जब इस प्रभाव को शामिल किया जाता है, तो यह पाया जाता है कि तापमान टी पर कृष्णिका वी वेग के साथ कम हो रहा है, जिससे लगता है कि टी तापमान पर स्थिर कृष्णिका के समान वर्णक्रम वाला होता है। जैसे[28]
एक ऐसे मामले, जिसमें स्रोत सीधे पर्यवेक्षक की ओर या उससे दूर सीधे जा रहा हो तो यह कम हो जाता है
यहाँ v >0 संकेत करता है कि यह कम हो रहा स्रोत है और v <0 निकट आ रहे स्रोत की ओर संकेत करता है।
यह खगोल विज्ञान में एक महत्वपूर्ण प्रभाव है, जहां सितारों और आकाशगंगाओं का वेग सी के महत्वपूर्ण अंशॉ तक पहुंच सकता है। ब्रह्मांडीय सूक्ष्म तरंग पृष्ठभूमि विकिरण में एक उदाहरण पाया गया है, जो इस कृष्णिका के विकिरण क्षेत्र के सापेक्ष पृथ्वी की गति से एक द्विध्रुवीय असमदिग्वर्ती होने की दशा (डाइपोल एनिसोट्रोफी) प्रदर्शित करता है।
इन्हें भी देखें[संपादित करें]
- कृष्णिका विकिरण
- बोलोमीटर
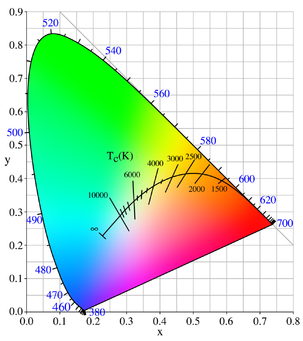
- रंग तापमान
- प्रभावी तापमान
- एमिसीविटी
- इन्फ्रारेड थर्मामीटर
- फोटोन ध्रुवीकरण
- पाइरोमेट्री
- रेले-जीन्स लॉ
- सुपर ब्लैक
- थर्मल विकिरण
- थरमॉग्राफी
- अल्ट्रावायोलेट कैटेस्ट्रॉफी
- सकुमा-हटोरी समीकरण
स[संपादित करें]
सन्दर्भ त्रुटि: <references> चिप्पि में अमान्य प्राचल
सन्दर्भ[संपादित करें]
- ↑ जी. किरचौफ (1896). रौशनी और गर्मी के लिए विभिन्न पदार्थों के विकिरणशील और अवशोषक के बीच संबंध पर फिल.मैग में एफ. गुथरी द्वारा अनुवादित. श्रृंखला 4, खंड 20, नं 130, पृष्ठ 1-21, मौलिक रूप में यह पोगेंन डौर्फ़ के एन्नालेन से उद्धृत है, खंड 109, पृष्ठ 275 एट सेक
- ↑ एम. प्लांक (1914). द थियुरी ऑफ़ हीट रेडियेशन दूसरा संस्करण. एम. मैसिअस, ब्लैकिसटन्स सन एंड कंपनी, फिलाडेल्फिया द्वारा अनुवादित,
- ↑ Robitaille, P. (2003). "On the validity of Kirchhoff's law of thermal emission". IEEE Transactions on Plasma Science. 31: 1263. डीओआइ:10.1109/TPS.2003.820958.
- ↑ "Science: Draper's Memoirs". The Academy. London: Robert Scott Walker. XIV (338): 408. Oct. 26, 1878.
|date=में तिथि प्राचल का मान जाँचें (मदद) - ↑ J. R. Mahan (2002). Radiation heat transfer: a statistical approach (3rd संस्करण). Wiley-IEEE. पृ॰ 58. आई॰ऍस॰बी॰ऍन॰ 9780471212706.
- ↑ Huang, Kerson (1967). Statistical Mechanics. New York: John Wiley & Sons.
- ↑ Planck, Max (1901). "On the Law of Distribution of Energy in the Normal Spectrum". Annalen der Physik. 4: 553. मूल ([मृत कड़ियाँ]) से 18 अप्रैल 2008 को पुरालेखित. अभिगमन तिथि 13 सितंबर 2010.
- ↑ Landau, L. D.; E. M. Lifshitz (1996). Statistical Physics (3rd Edition Part 1 संस्करण). Oxford: Butterworth-Heinemann.
- ↑ मैथेमैटिका: प्लांक आधिक्य (एनर्जी/सेक/एरिया/सॉलीड एंगल/वेवलेंथ) है:
i[w_, t_] = 2*h*c^2/(w^5*(Exp[h*c/(w*k*t)] - 1))
फोतोंस/सेक/एरिया की संख्या है:
NIntegrate[2*Pi*i[w, 300]/(h*c/w), {w, 390*10^(-9), 750*10^(-9)}] = 0.0244173... - ↑ इलेक्ट्रो ऑप्टिकल इंडस्ट्रीज, Inc (2008) ब्लैकबॉडी एयर इन्फ्रारेड विकिरण क्या होता है Archived 2016-03-07 at the वेबैक मशीन? शिक्षा के सन्दर्भ में
- ↑ K. Mizuno; एवं अन्य (2009). "A black body absorber from vertically aligned single-walled carbon nanotubes" (free download). Proceedings of the National Academy of Sciences. 106 (15): 6044–6077. PMID 19339498. डीओआइ:10.1073/pnas.0900155106. पी॰एम॰सी॰ 2669394. Explicit use of et al. in:
|author=(मदद) - ↑ Nave, Dr. Rod. "Wien's Displacement Law and Other Ways to Characterize the Peak of Blackbody Radiation". HyperPhysics. मूल से 18 मार्च 2011 को पुरालेखित. वायेन के विस्थापना नियम के 5 भिन्नरूप प्रदान करता है
- ↑ Infrared Services. "Emissivity Values for Common Materials". मूल से 25 जून 2007 को पुरालेखित. अभिगमन तिथि 24 जून 2007.
- ↑ Omega Engineering. "Emissivity of Common Materials". मूल से 28 जून 2007 को पुरालेखित. अभिगमन तिथि 24 जून 2007.
- ↑ Farzana, Abanty (2001). "Temperature of a Healthy Human (Skin Temperature)". The Physics Factbook. मूल से 29 जून 2007 को पुरालेखित. अभिगमन तिथि 24 जून 2007.
- ↑ Lee, B. "Theoretical Prediction and Measurement of the Fabric Surface Apparent Temperature in a Simulated Man/Fabric/Environment System" (PDF). मूल (PDF) से 2 सितंबर 2006 को पुरालेखित. अभिगमन तिथि 24 जून 2007.
- ↑ Harris J, Benedict F (1918). "A Biometric Study of Human Basal Metabolism". Proc Natl Acad Sci USA. 4 (12): 370–3. PMID 16576330. डीओआइ:10.1073/pnas.4.12.370. पी॰एम॰सी॰ 1091498.
- ↑ Levine, J (2004). "Nonexercise activity thermogenesis (NEAT): environment and biology". Am J Physiol Endocrinol Metab. 286 (5): E675–E685. PMID 15102614. डीओआइ:10.1152/ajpendo.00562.2003. मूल से 27 जून 2010 को पुरालेखित. अभिगमन तिथि 13 सितंबर 2010.
- ↑ DrPhysics.com. "Heat Transfer and the Human Body". मूल से 23 जून 2007 को पुरालेखित. अभिगमन तिथि 24 जून 2007.
- ↑ अ आ Cole, George H. A.; Woolfson, Michael M. (2002). Planetary Science: The Science of Planets Around Stars (1st ed.). Institute of Physics Publishing. पपृ॰ 36–37, 380–382. आई॰ऍस॰बी॰ऍन॰ 0-7503-0815-X.सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)
- ↑ अ आ इ "नासा सन फैक्ट शीट". मूल से 15 जुलाई 2010 को पुरालेखित. अभिगमन तिथि 13 सितंबर 2010.
- ↑ Saari, J. M.; Shorthill, R. W. (1972). "The Sunlit Lunar Surface. I. Albedo Studies and Full Moon". The Moon. 5 (1–2): 161–178. डीओआइ:10.1007/BF00562111. मूल से 23 अक्तूबर 2013 को पुरालेखित. अभिगमन तिथि 13 सितंबर 2010.
- ↑ लूनर और ग्रह विज्ञान XXXVII (2006) 2406
- ↑ Michael D. Papagiannis (1972). Space physics and space astronomy. Taylor & Francis. पपृ॰ 10–11. आई॰ऍस॰बी॰ऍन॰ 9780677040004.
- ↑ Willem Jozef Meine Martens and Jan Rotmans (1999). Climate Change an Integrated Perspective. स्प्रिंगर. पपृ॰ 52–55. आई॰ऍस॰बी॰ऍन॰ 9780792359968.
- ↑ F. Selsis (2004). "The Prebiotic Atmosphere of the Earth". प्रकाशित Pascale Ehrenfreund; एवं अन्य (संपा॰). Astrobiology: Future Perspectives. स्प्रिंगर. पपृ॰ 279–280. आई॰ऍस॰बी॰ऍन॰ 9781402025877. Explicit use of et al. in:
|editor=(मदद) - ↑ द डोपलर प्रभाव, टी.पी.गिल, लोगोस प्रेस, 1965
- ↑ McKinley, John M. (1979). "Relativistic transformations of light power". American Journal of Physics. 47: 602. डीओआइ:10.1119/1.11762.
अन्य पाठ्यपुस्तकें[संपादित करें]
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd संस्करण). W. H. Freeman Company. आई॰ऍस॰बी॰ऍन॰ 0716710889.सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th संस्करण). W. H. Freeman. आई॰ऍस॰बी॰ऍन॰ 0716743450.सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)
बाहरी कड़ियाँ[संपादित करें]
- ब्लैकबॉडी रेडिएशन की गणना डोपलर एफेक्ट के साथ इंटरएक्टिव कैलकुलेटर. इकाइयों के अधिकांश सिस्टम भी शामिल हैं।
- हाइपरफिसिक्स द्वारा मानव शरीर के लिए शीतलक तंत्र
- कई अलग-अलग वस्तुओं द्वारा उत्सर्जित विकिरण का वर्णन
- ब्लैकबॉडी एमिशन एप्प्लेट
- "ब्लैकबॉडी स्पेक्ट्रम" जेफ़ ब्राइयंट द्वारा वुल्फ्रम डेमोंसट्रेशन्स प्रोजेक्ट, २००७.
- कार्बन नैनो टियूब ब्लैकबॉडी (एआईएसटी (AIST) नैनो टेक 2009)


































