समान्तर अक्ष का प्रमेय
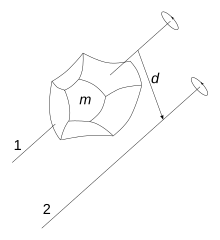
गति विज्ञान में समान्तर अक्ष का प्रमेय (parallel axis theorem) या स्टीनर का प्रमेय (Steiner's theorem) जड़त्वाघूर्ण से सम्बन्धित एक प्रमेय है। यदि किसी पिण्ड के द्रव्यमान केन्द्र से जाने वाली किसी अक्ष के सापेक्ष उस पिण्ड का जड़त्वाघूर्ण ज्ञात हो तो इस प्रमेय की सहायता से इस अक्ष के समान्तर किसी भी अक्ष के सापेक्ष उस पिण्ड का जड़त्वाघूर्ण निकाला जा सकता है।
माना कि:
Icm पिण्ड के द्रव्यमान केन्द्र से जाने वाली किसी अक्ष के सापेक्ष जड़त्वाघूर्ण है,
M पिण्ड का द्रव्यमान है तथा d नये एवं पुराने (दिये हुए) अक्षों के बीच की लम्बवत दूरी है
तो नये अक्ष z के परित: पिण्ड का जड़त्वाघूर्ण निम्नलिखित समीकरण की सहायता से पाया जा सकता है-:
इस समीकरण का उपयोग स्ट्रेच नियम (stretch rule) तथा लम्बवत अक्ष का प्रमेय (perpendicular axis theorem) के साथ करके अनेकानेक स्थितियों में जड़त्वाघूर्ण की गणना की जा सकती है।

समान्तर अक्ष के प्रमेय का प्रयोग किसी समतल क्षेत्र D का क्षेत्राघूर्ण निकालने के लिये भी किया जा सकता है।:
इन्हें भी देखें[संपादित करें]
- लम्बवत अक्ष का प्रमेय (Perpendicular axis theorem)
- जड़त्वाघूर्ण


