चरघातांकी बंटन

चरघातांकी

संचयी बंटन फलन
प्राचल	$\lambda >0,$ दर अथवा व्युत्क्रम पैमाना
आधार	$x\in [0,\infty )$
	$\lambda e^{-\lambda x}$
संचयी बंटन फलन	$1-e^{-\lambda x}$
माध्य	${\frac {1}{\lambda }}$
माध्यिका	${\frac {\ln 2}{\lambda }}$
बहुलक	$0$
	${\frac {1}{\lambda ^{2}}}$
वैषम्य	$2$
अधि वक्रता-मात्रा	$6$
एन्ट्रॉपी	$1-\ln \lambda$
आघूर्णजनक फलन	${\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda$
अभिलक्षणिक-फलन	${\frac {\lambda }{\lambda -it}}$
मत्स्य सूचना	${\frac {1}{\lambda ^{2}}}$

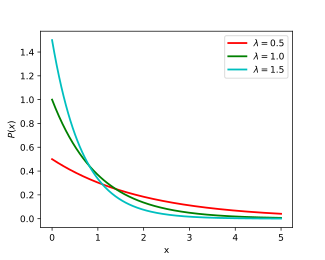
प्रायिकता सिद्धांत और सांख्यिकी में चरघातांकी बंटन (exponential distribution) अथवा नकारात्मक चरघातांकी बंटन (negative exponential distribution) प्वासों बिन्दु प्रक्रिया की घटनाओं के मध्य की दूरी के लिए एक प्रायिकता बंटन है। अर्थात् यह बंटन उन प्रक्रियाओं के लिए है जिनमें प्रेक्षित बिन्दु नियत माध्य दर पर सतत और स्वतंत्र हैं; दूरी प्राचल प्रक्रिया का सार्थक एक-विमीय मापन है जैसे बुनाई निर्माण प्रक्रिया में कपड़े के रोल की लम्बाई अथवा उत्पादन त्रुटि के मध्य समय। यह गामा बंटन का एक उदाहरण है। यह ज्यामितीय बंटन का सतत रूप है। प्वासों बिन्दु प्रक्रिया के विश्लेषण में काम आने के अतिरिक्त अन्य विभिन्न प्रसंगों में भी यह उपयोगी है।

चरघातांकी बंतन चरघातांकी परिवार के अन्य बंटनों के समान नहीं है। यह प्रायिकता बंटनों का बड़ा वर्ग है जिसमें चरघातांकी बंटन भी एक है। लेकिन इसमें और भी बहुत बंटन शामिल हैं जैसे प्रसामान्य, द्विपद, गामा और प्वासों बंटन शामिल हैं।

परिभाषा

प्रायिकता घनत्व फलन

चरघातांकी बंटन का प्रायिकता घनत्व फलन (pdf)

$f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

जहाँ λ > 0 बंटन का प्रचाल है, अक्सर इसे दर प्राचल कहते हैं। बंटन [0, ∞) अंतराल में वैध है। यदि यह बंटन यादृच्छिक चर X का है तो  X ~ Exp(λ) होगा।

चरघातांकी बंटन अनंत विभाज्य रखताता है।

संचयी बंटन फलन

संचयी बंटन फलन इस प्रकार लिखा जाता है

$F(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

वैकल्पिक प्राचलीकरण

चरघातांकी बंटन को कभी-कभी पैमाना प्राचल β = 1/λ से प्राचलित किया जाता है $$f(x;\beta )={\begin{cases}{\frac {1}{\beta }}e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}\qquad \qquad F(x;\beta )={\begin{cases}1-e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}$$

गुणधर्म

माध्य, विचलन, आघुर्ण और माध्यिका

प्रायिकता द्रव्यमान केन्द्र का माध्य, प्रथम आघुर्ण

पूर्वप्रतिबिम्ब F⁻¹(1/2) की माध्यिका।

दर प्राचल λ के यादृच्छिक चर X के चरघातांकी बंटन के प्रत्याशा मान का माध्य $$\operatorname {E} [X]={\frac {1}{\lambda }}.$$

यदि कोई व्यक्ति प्रतिघंटे दो बार फोन कर रहा है तो सम्भावित है कि वो हर आधे घंटे में एक बार फोन करेगा।

X का प्रसरण $$\operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},$$ अतः मानक विचलन का मान माध्य के बराबर है।

$n\in \mathbb {N}$ के लिए X का आघुर्ण $$\operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.$$

$n\in \mathbb {N}$ के लिए X का केन्द्रीय आघूर्ण $$\mu _{n}={\frac {!n}{\lambda ^{n}}}={\frac {n!}{\lambda ^{n}}}\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.$$ जहाँ !n चर n का उप-क्रमगुणित है।

X की माध्यिका $$\operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],$$ जहाँ ln प्राकृतिक लघुगणक है। अतः माध्य और माध्यिका में पूर्ण अन्तर $$\left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],$$