वर्णनात्मक ज्यामिति
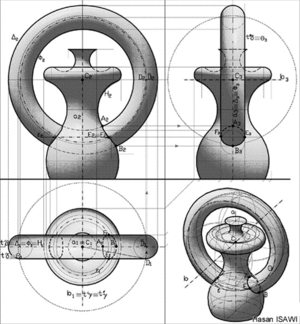

ठोसों, तलों, रेखाओं और उनके प्रतिच्छेदों के परिमाण, आकार और स्थिति की दृष्टि से, यथार्थ रेखण को वर्णनात्मक ज्यामिति (Descriptive Geometry) कहते हैं। फ्रांसीसी गणितज्ञ और भौतिकविद्, गैसपर्ड मॉंज (Gaspard Monge), ने १८वीं शताब्दी के अंत में इस व्यावहारिक ज्यामिति का आविष्कार किया। सभी वास्तुनिर्माण और यांत्रिकी मानचित्रण का यह सैद्धांतिक आधार है और इसका उपयोग मशीनों, इमारतों, पुलों तथा जहाजों के नक्शे खींचने में, छाया के निरूपण में तथा गोलीय त्रिभुजों के आलेखीय हल में किया जाता है। इसके माध्यम से अभिकल्पी अपने विचार इस विद्या में निपुण राज और मिस्त्री को समझाता है। इसी लिये वर्णनात्मक ज्यामिति को इंजीनियर की सार्वदेशिक भाषा कहा गया है।
वर्णात्मक ज्यामिति द्वारा पिंडों से संबंधित समस्या के हल में ये बातें आवश्यक हैं :
- (१) रेखाओं, पृष्ठों या ठोसों का समतलीय आकृतियों द्वारा निरूपण,
- (२) इन आकृतियों की सहायता से समस्या को हल करना और अंत में
- (३) इस हल को त्रिविमितीय पिंडों के संदर्भ में समझना। समतलीय निरूपण लंबरेखी प्रक्षेप (orthographic projection) के अनुसार किया जाता है। समतल पर किसी वस्तु (बिंदु, रेखा, तल या ठोस कुछ भी हो) का लंबरेखी प्रक्षेप वह आकृति है जो उस वस्तु के प्रत्येक बिंदु से दिए हुए समतल पर खींचे गए अभिलंबों के पादों से बनती है। इस प्रकार समतल पर किसी ऋजु रेखा अ ब (AB) का लंबरेखी प्रक्षेप सामान्यता एक ऋजु रेखा ही होगी; यदि अ ब (AB) समतल पर लंबे है तो प्रक्षेप बिंदु मात्र होगा; यदि समतल के समांतर है तो प्रक्षेप द्वारा उतनी बड़ी रेखा मिलेगी, अन्यथा कुछ छोटी।
समतल पर तिर्यक् प्रक्षेप भी हो सकता है; तब प्रक्षेप वस्तु के विभिन्न बिंदुओं से समांतर रेखाएँ अभिलंब दिशा के अतिरिक्त किसी अन्य दिशा में खींची जाती हैं। तिर्यक् प्रक्षेप का उपयोग छायाचित्रण के लिये किया जाता है। कैसा भी प्रक्षेप हो, प्रक्षेपण के लिये खींची गई समांतर रेखाओं को प्रक्षेपक, अथवा किरण, कहते हैं। समांतर किरणों से प्राप्त प्रक्षेपण में प्रक्षेप का परिमाण प्रक्षेप्य की दूरी पर निर्भर नहीं करता।
यदि सभी प्रक्षेपक किरणें एक बिंदु से, जिसे दृष्टिबिंदु कहते हैं, लेकर जाएँ, तो दृश्यलेखी प्रक्षेप (seenographic projection), अथवा संदर्श (perspective), मिलता है। इस प्रकार वस्तु का ऐसा चित्र बनता है जैसा वह नेत्र को दिखाई देती है। दृष्टिबिंदु और प्रक्षेप समतल दोनों से वस्तु की दूरियों पर इस चित्र का परिमाण निर्भर करता है। सामान्यतया प्रेक्षप से लंबरेखी प्रक्षेप का आशय होता है।
वस्तुनिरूपण की मॉंज विधि में वस्तु के दो, या कभी-कभी अधिक, समतलों पर लंबरेखी प्रक्षेप लिए जाते हैं। मुख्य समतल दो है : ऊर्ध्वाधर समतल, जिसे ऊ (V) से सूचित करते हैं और क्षैतिज, जिसे क्ष (H) से व्यक्त करते हैं। इन समतलों की प्रक्षेप रेखा को आधार रेखा (groundline) कहते हैं और आ रे (GL) से सूचित करते हैं। कभी-कभी तीसरे समतल पार्श्वतल (profile plane) की आवश्यकता होती हे, तब इसे आ रे (GL) के लंब रूप में लिया जाता है और यह ऊतथा क्ष दोनों समतलों पर लंब होता है।
ऊर्ध्वाधर समतलवाले प्रक्षेप को ऊ-प्रक्षेप या संमुखदर्शन (elevation) कहते हैं और क्षैतिज समतलवाले को क्ष-प्रक्षेप या अनुविक्षेप (plan) कहते हैं। संमुखदर्शन के स्थान पर पृष्ठदर्शन, अथवा अनुप्रस्थ दर्शन, भी लिया जाता है तथा अनुविक्षेप के स्थान में शीर्षस्थ, अथवा तलदर्शन, अथवा अनुप्रस्थ विक्षेप भी लिया जाता है। और इन शब्दों का ही व्यवहार स्पष्टता के लिये कर दिया जाता है। इसी प्रकार पार्श्वदर्शन को अंतदर्शन (end view) भी कहते हैं।
मुख्य प्रक्षेप समतलों को विस्तार में अनंत माना जाता है। इनसे आकाश चार भागों में, जिन्हें चतुर्थांश (quardrants) कहते हैं, विभक्त हो जाता है। द्रष्टा और ऊर्ध्वाधर समतल के बीचवाले चुतर्थांशों से क्षैतिज समतल से ऊपरवाले को प्रथम और नीचेवाले को चुतर्थ कहते हैं। ऊर्ध्वाधर समतल से पीछे के चतुर्थांशों में से ऊपरवाले को द्वितीय और नीचेवाले को तृतीय कहते हैं। त्रिविमितीय आकाश में स्थित किसी बिंदु ब को समतल पर निरूपित करने के लिये ब से दोनों मुख्य समतलों पर अभिलंब खींचे जाते हैं। मान लें, इनके पाद ऊर्ध्वाधर समतल पर ब ऊऔर क्षैतिज पर ब क्ष हैं। अब ऊर्ध्वाधर समतल को आ रे (GL) के परित: चतुर्थांश १ से २ की ओर घुमाकर क्षैतिज स्थिति में ले आया जाता है और बऊ की यह स्थिति तथा बक्ष की मूल स्थिति समतल पर बिंदु ब को निरूपित करती हैं।
वास्तुशिल्पी रेखण में पिंड को प्रथम चतुर्थांश में स्थित मान लिया जाता है। फलत: सम्मुखदर्शन अनुविक्षेप के ऊपर रहता है। इंजीनियरी रेखण में पिंड को तृतीय चतुर्थांश में और संदर्श रेखण में द्वितीय चतुर्थांश में स्थित मानते हैं। चतुर्थ चतुर्थांश का कदाचित् ही व्यवहार होता है।
उपर्युक्त विधि से ऋजुरेखा का प्रक्षेप सदा ऋजुरेखा ही मिलेगा। अनंत समतल को प्रक्षेप द्वारा निरूपित नहीं किया जा सकता, क्योंकि उसका प्रक्षेप दोनों मुख्य समतलों को ढक देगा। अत: समतल को उसकी और मुख्य समतलों की प्रतिच्छेद रेखाओं द्वारा निरूपित किया जाता है, जिन्हें अनुरेख (traces) कहते हैं। यदि समतल किसी भी मुख्य समतल के समांतर नहीं है तो इसके अनुरेखण या तो आ रे (GL) के समांतर होंगे, या आ रे (GL) को एक ही बिंदु पर काटेंगे। आ रे (GL) से जानेवाले समतल को पार्श्व समतलवाले अनुरेख द्वारा निरूपित किया जाता है।
पृष्ठों और उनके प्रतिच्छेद वक्रों का निरूपण उनके विभिन्न परिच्छेदों के प्रक्षेपों द्वारा किया जाता है। विकासनीय पृष्ठ विशेष रूप से इस विधि द्वारा निरूपणगम्य होते हैं। छाया और प्रतिच्छायाओं के निरूपण के लिये प्रकाश किरणों को समांतर और द्रष्टा के बाएँ कंधे पर से ऐसी दिशा में आती हुई माना जाता है कि मुख्य समतलों पर उनके प्रक्षेप आधार रेखा से ४५o के कोण बनाते हैं। प्रच्छाया, उपच्छाया, छायारेखा तथा प्रकाशित भाग वर्णनात्मक ज्यामिति द्वारा सरलता से निरूपित किए जा सकते हैं। इंजीनियरी छात्रों के लिये यह पाठ्यक्रम का विषय है और अनेक प्राविधिक तथा शैक्षिक पुस्तकें इसपर उपलब्ध हैं।
इन्हें भी देखें[संपादित करें]
- प्रक्षेप (प्रोजेक्शन)
- ठोस ज्यामिति
- अवकल ज्यामिति
- निर्देशांक ज्यामिति या विश्लेषणात्मक ज्यामिति या वैश्लेषिक ज्यामिति
संदर्भ ग्रंथ[संपादित करें]
- जेo एo बेनेट : डेस्क्रिप्टिव ज्यॉमेट्री (१९६१);
- सीo ईo डगलस ऐंड एo एलo होग : डेस्क्रिप्टिव ज्याँमेट्री (१९६२)
