आरेख

किसी सूचना का किसी दृष्य-तकनीक के अनुसार द्विविमीय (2D) ज्यामिति में सांकेतिक अभिव्यक्ति संरेखी, या आरेख (diagram) कहलाता है। कभी-कभी इसे ग्राफ नाम से भी पुकारते हैं। आरेख वह चित्र है जिसके विभिन्न भागों के परस्पर सम्बन्ध आरेख से निरूपित वस्तुओं के परस्पर सम्बन्ध को स्पष्ट करते हैं तथा उन सम्बन्धों को जो चित्र से आरेखी रीति से अभिव्यक्त नहीं होते, चित्र में अंकित संख्याओं अथवा अन्य प्रविष्टियों द्वारा दिखाते हैं।
किसी आरेख का अभिप्राय उन मुख्य सम्बन्धों को नेत्रों के समक्ष स्पष्ट रूप से प्रस्तुत करना है जिनपर ध्यान आकर्षित करना हो और कभी-कभी आरेख से अभिव्यक्त वस्तु से सम्बन्धित कुछ महत्वपूर्ण राशियों के यथार्थ संख्यात्मक मान को, चित्र पर माप द्वारा, दिखाना है।
आरेख के प्रमुख प्रकार[संपादित करें]
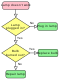
ग्राफ पर आधारित आरेख[संपादित करें]
|
|
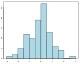
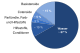
चार्ट-जैसी तकनीकें[संपादित करें]
|
|
अन्य प्रकार के आरेख[संपादित करें]
- Maps (when stylized, e.g. the map of the London underground)
- exploded view
|
|
प्रमुख आरेख[संपादित करें]
प्रत्यय की व्यापकता के कारण, आरेख अनेक प्रकार के विशिष्ट अभिप्राय को व्यक्त करने में लाभादायक होते हैं। कुछ आरेख निम्नलिखित हैं :
(
आरेख गणितीय लेखों में आरेखों का प्रयोग विशेष रूप से इस कारण किया जाता है कि पाठक को तर्क समझ में आ जाए। एक अच्छा आरेख वह समझा जाता है जो साध्य के मुख्य लक्षणों को स्पष्ट रूप से प्रकट कर सके। प्राय: गणित में आरेख का वर्णन शब्दों में इतने स्पष्ट ढंग से करते हैं कि पाठक उसको स्वयं भी खींच सकता है। यांत्रिकी में आरेख अधिकतम प्रकार के अभिप्रायों से उपयोग किए जाते हैं। स्थैतिकी में इनका प्रयोग अत्यधिक सुविधाजनक है, क्योंकि किसी स्थैतिक तंत्र के भाग गतिशील नहीं होते।
(2) रसायन में आरेख जॉन डाल्टन ने परमाणु विन्यास सम्बन्धी अपनी संकल्पना में अनेक सामान्य यौगिकों के आरेख प्रकाशित किए। उस समय से इनका प्रयोग रसायनज्ञों द्वारा बहुत मात्रा में किया जा रहा है। इसी भाँति क्रिस्टलकी में क्रिस्टल संरचना की व्याख्या में आरेखों का प्रयोग बहुधा किया जाता है।
(3) मापक आरेख : आरेख का प्रयोग मापने में भी करते हैं। इस प्रकार के आरेख का अभिप्राय निदर्शन के अतिरिक्त यथार्थ मापन भी होता है।
(4) त्रिविमितीय वस्तु आरेख : किसी दो से अधिक चर राशियों पर निर्भर परिमाणों के कुलक के लेखाचित्र-प्रदर्शन के लिये आरेख पद्धति का प्रयोग सम्भव है। विशेषत: किसी त्रिविमितीय वस्तु के अंगो के परस्पर सम्बन्धों को निरूपित करने के लिये दो अथवा अधिक आरेखों का प्रयोग कर सकते हैं। इस प्रकार की आरेख पद्धति में एक ऐसे निश्चित संकेत की आवश्यकता होती है। जिससे यह ज्ञात होता है कि आरेख किस प्रकार से पूर्ण संरचना से तथा आपस में पृथकत: सम्बन्धित हैं। इमारत और पुल के मानचित्र इसके उदाहरण हैं। ठोस एवं अन्य त्रिविमितीय आकृति को भी एकल आरेख से निरूपित कर सकते हैं।
अन्य आरेख[संपादित करें]
कुछ अन्य आरेखों का संक्षिप्त विवरण निम्नलिखित है :
(क) आर्गड - चित्र में संमिश्र संख्या न्अत्न्र् को किसी निर्देशांक पद्धति के निर्देश में संगत बिंदु (x,y) ये निरूपित करते हैं।
(ख) स्वचालित आरेख वह है, जो किसी मशीन से स्वत: निर्मित हो जाता है और दो चर राशियों में सम्बन्धित विचरण को दिखाता है; उदाहरणार्थ, दिन पर्यत के ताप में परिवर्तन।
(ग) ऐंट्रॉपी आरेख किसी ऊष्मागतिक चक्र में ऐंट्रॉपी परिवर्तन दिखाता है।
(घ) फ्रेम-आरेख में बिंदुओं को बिंदुओं से और जोड़नेवाली कड़ी को रेखा से निरूपित करते हैं।
(च) हेर्ट्ज-आरेख निर्दिष्ट हवा की मात्रा में ताप, दाब और नमी के परिवर्तन को, जबकि हवा के आयतन में रुद्धोष्म परिवर्तन हो रहा ही, निरूपित करता है। "नायहोफ आरेख" इसी के अनुरूप होता है।
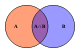
(छ) ऑयलर आरेख तार्किक सम्बन्धों का आलेखी निरूपण करता है। इसमें वृत्त अथवा अन्य चित्रों द्वारा उन राशियों की श्रेणी को सूचित करते हैं जिनपर निर्दिष्ट गुण लागू होते हैं।
(ज) विकृति आरेख एक चित्र है, जो किसी प्रतिबल के परिमाण और उसके कारण उत्पन्न विकृति को निरूपित करता है।
"आरेख" शब्द का अनेकान्य प्रसंगों में प्रयोग करते हैं, जिनमें से बहुत से स्वत: स्पष्ट होते हैं।
विशिष्ट प्रकार के आरेख[संपादित करें]
आरेख बनाने के हजारों तरीके प्रचलन में हैं। नीचे कुछ उदाहरण दिये जा रहे हैं-
इन्हें भी देखें[संपादित करें]
- व्य्वस्था आरेख (schematic diagram)
- चार्ट (Chart)
- सचित्र तर्क (Diagrammatic reasoning)
- ग्राफीय विधियों की सूची (List of graphical methods])
- गणितीय आरेख (Mathematical diagram)
सन्दर्भ aarakka[संपादित करें]
- ↑ "HIPO diagram". मूल से 5 फ़रवरी 2009 को पुरालेखित. अभिगमन तिथि 30 अगस्त 2009.
पठनीय सामग्री[संपादित करें]
- Michael Anderson, Peter Cheng, Volker Haarslev (Eds.) (2000). Theory and Application of Diagrams: First International Conference, Diagrams 2000. Edinburgh, Scotland, UK, September 1-3, 2000. Proceedings.