क्रमगुणित

क्रमगुणित:- 1 से लेकर n तक की लगातार संख्याओं के गुणनफल को क्रमगुणित कहते हैं। इसे n! से दर्शाते हैं।

n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
70	1.197857167×१०100
100	9.332621544×१०157
450	1.733368733×१०1,000
1000	4.023872601×१०2,567
3249	6.412337687×१०10,000
10000	2.846259681×१०35,659
25206	1.205703438×१०1,00,000
100000	2.824229408×१०4,56,573
205023	2.503898931×१०10,00,004
1000000	8.263931687×१०55,65,708
1723508	5.290070307×१०1,00,00,001
2000000	3.776821058×१०1,17,33,474
10000000	1.2024234×१०6,56,57,059
14842907	2.788662974×१०10,00,00,000

गणित में किसी अऋणात्मक पूर्णांक n का क्रमगुणित या 'फैक्टोरियल' वह संख्या है जो उस पूर्णांक n तथा उससे छोटे सभी धनात्मक पूर्णांकों के गुननफल के बराबर होता है। इसे n!, से निरूपित किया जाता है। उदाहरण के लिये,

$5!=5\times 4\times 3\times 2\times 1=120\$

0! का मान is 1 होता है।

गणित के अनेकों क्षेत्रों में क्रमगुणित का उपयोग करना पड़ता है, जिनमें से क्रमचय-संचय, बीजगणित तथा गणितीय विश्लेषण प्रमुख हैं।

इतिहास

क्रमगुणित की अवधारणा कई संस्कृतियों में स्वतंत्र रूप से उत्पन्न हुई है:

• भारतीय गणित में, फैक्टोरियल का सबसे पहला ज्ञात विवरण अनुयोगद्वार-सूत्र से आता है, जो जैन साहित्य के प्रामाणिक कार्यों में से एक है, जिसे 300 ईसा पूर्व से 400 ईसवी तक की तिथियां दी गई हैं। यह वस्तुओं के एक समूह के क्रमबद्ध और उलटे क्रम को अन्य ("मिश्रित") क्रमों से अलग करता है, तथा क्रमगुणित के लिए सामान्य उत्पाद सूत्र से दो घटाकर मिश्रित ऑर्डर की संख्या का मूल्यांकन करता है। क्रमचय के लिए गुणन नियम का वर्णन 6वीं शताब्दी ई. के जैन भिक्षु जिनभद्र ने भी किया था। हिंदू विद्वान कम से कम ११५० के बाद से क्रमगुणित सूत्रों का उपयोग कर रहे हैं, जब भास्कर द्वितीय ने अपने काम लीलावती में क्रमगुणित का उल्लेख किया था, एक समस्या के संबंध में कि विष्णु अपने चार विशिष्ट वस्तुओं (शंख, चक्र, गदा, और कमल का फूल) को अपने चार हाथों में कैसे पकड़ सकते हैं, और दस-हाथ वाले भगवान के लिए एक समान समस्या।

• मध्य पूर्व के गणित में, सृष्टि की हिब्रू रहस्यवादी पुस्तक सेफर यतिजिराह, जो कि तल्मूडिक काल (200 से 500 ई.) की है, में 7! तक के क्रमगुणित की सूची दी गई है, जो कि हिब्रू वर्णमाला से बनने वाले शब्दों की संख्या की जांच का एक हिस्सा है। 8वीं शताब्दी के अरब व्याकरणविद अल-खलील इब्न अहमद अल-फ़राहिदी ने भी इसी तरह के कारणों से क्रमगुणित का अध्ययन किया था। अरब गणितज्ञ इब्न अल-हेथम (जिन्हें अलहाज़ेन के नाम से भी जाना जाता है, सी. 965 - सी. 1040) क्रमगुणित को अभाज्य संख्या से जोड़ने वाले विल्सन प्रमेय को तैयार करने वाले पहले व्यक्ति थे।

• यूरोप में, हालांकि यूनानी गणित में कुछ संयोजन शामिल थे, और प्लेटो ने एक आदर्श समुदाय की जनसंख्या के रूप में 5,040 (एक क्रमगुणित) का इस्तेमाल किया था, आंशिक रूप से इसकी विभाज्यता गुणों के कारण, क्रमगुणित के प्राचीन ग्रीक अध्ययन का कोई प्रत्यक्ष प्रमाण नहीं है। इसके बजाय, यूरोप में क्रमगुणित पर पहला काम यहूदी विद्वानों जैसे कि शब्बेथाई डोनोलो द्वारा किया गया था, जिसमें सेफर यतिज़िराह मार्ग की व्याख्या की गई थी। 1677 में, ब्रिटिश लेखक फेबियन स्टेडमैन ने चेंज रिंगिंग में क्रमगुणित के अनुप्रयोग का वर्णन किया, जो एक संगीत कला है जिसमें कई ट्यून की गई घंटियों को बजाना शामिल है।

15वीं शताब्दी के उत्तरार्ध से क्रमगुणित पश्चिमी गणितज्ञों के अध्ययन का विषय बन गया। 1494 के एक ग्रंथ में, इतालवी गणितज्ञ लुका पसिओली ने डाइनिंग टेबल व्यवस्था की एक समस्या के संबंध में 11! तक के क्रमगुणित की गणना की। क्रिस्टोफर क्लैवियस ने जोहान्स डी सैक्रोबोस्को के काम पर 1603 की एक टिप्पणी में फैक्टोरियल पर चर्चा की, और 1640 के दशक में, फ्रांसीसी पॉलीमैथ मैरिन मर्सेन ने क्लैवियस के काम के आधार पर, 64! तक के फैक्टोरियल की बड़ी (लेकिन पूरी तरह से सही नहीं) सारणियां प्रकाशित कीं। घातांकीय फलन के लिए घात श्रेणी, इसके गुणांकों के लिए फैक्टोरियल के पारस्परिक के साथ, पहली बार 1676 में आइजैक न्यूटन द्वारा गॉटफ्रीड विल्हेम लीबनिज को लिखे एक पत्र में तैयार किया गया था। क्रमगुणित पर प्रारंभिक यूरोपीय गणित के अन्य महत्वपूर्ण कार्यों में जॉन वालिस द्वारा 1685 के ग्रंथ में व्यापक कवरेज, अब्राहम डी मोइवर द्वारा 1721 में $n$ के बड़े मूल्यों के लिए उनके अनुमानित मूल्यों का एक अध्ययन, जेम्स स्टर्लिंग द्वारा डी मोइवर को 1729 का एक पत्र जिसमें बताया गया था कि स्टर्लिंग का सन्निकटन के रूप में क्या जाना जाता है, और डैनियल बर्नौली और लियोनहार्ड यूलर द्वारा उसी समय क्रमगुणित फलन के गामा फलन तक निरंतर विस्तार को सूत्रबद्ध करने का कार्य शामिल है। एड्रियन-मैरी लीजेंड्रे ने लीजेंड्रे का सूत्र शामिल किया, जिसमें अभाज्य घातों में क्रमगुणित के कारकीकरण में घातांकों का वर्णन किया गया था, संख्या सिद्धांत पर 1808 के एक पाठ में।

क्रमगुणित के लिए संकेतन $n!$ फ्रांसीसी गणितज्ञ क्रिश्चियन क्रैम्प द्वारा 1808 में पेश किया गया था। कई अन्य संकेतन भी इस्तेमाल किए गए हैं। बाद के एक और संकेतन $\vert \!{\underline {\,n}}$, जिसमें क्रमगुणित का तर्क एक बॉक्स के बाएं और निचले हिस्से से आधा घिरा हुआ था, ब्रिटेन और अमेरिका में कुछ समय के लिए लोकप्रिय था, लेकिन इसका इस्तेमाल बंद हो गया, शायद इसलिए क्योंकि इसे टाइप करना मुश्किल है। "फैक्टोरियल" शब्द (मूल रूप से फ्रेंच: फैक्टोरियल) का पहली बार प्रयोग 1800 में लुई फ्रांकोइस एंटोनी आर्बोगास्ट द्वारा किया गया था, फाआ डी ब्रूनो के सूत्र पर पहले काम में, लेकिन अंकगणितीय प्रगति के उत्पादों की एक अधिक सामान्य अवधारणा का उल्लेख करते हुए। यह नाम जिन "कारकों" को संदर्भित करता है, वे क्रमगुणित के लिए गुणन सूत्र के पद हैं।

परिभाषा

एक धनात्मक पूर्णांक $n$ का क्रमगुणित फलन $n$ से छोटे सभी धनात्मक पूर्णांकों के गुणनफल द्वारा परिभाषित किया जाता है।

$$n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n.$$

इसे उत्पाद संकेतन में और अधिक संक्षिप्त रूप से इस प्रकार लिखा जा सकता है

$$n!=\prod _{i=1}^{n}i.$$

यदि इस गुणन सूत्र को अंतिम पद को छोड़कर बाकी सभी पदों को रखने के लिए बदल दिया जाता है, तो यह एक छोटे क्रमगुणित के लिए समान रूप का एक गुणनफल परिभाषित करेगा। यह एक पुनरावृत्ति संबंध की ओर ले जाता है, जिसके अनुसार क्रमगुणित फलन का प्रत्येक मान पिछले मान को $n$ से गुणा करके प्राप्त किया जा सकता है:

$$n!=n\cdot (n-1)!.$$

उदाहरण के लिए, $5!=5\cdot 4!=5\cdot 24=120$

शून्य का क्रमगुणित

$0$ का क्रमगुणित $1$ है, या प्रतीकों में, $0!=1$ है। इस परिभाषा के लिए कई प्रेरणाएँ हैं:

• $n=0$ के लिए, $n!$ की परिभाषा में गुणनफल के रूप में किसी भी संख्या का गुणनफल शामिल नहीं है, और इसलिए यह व्यापक सम्मेलन का एक उदाहरण है कि खाली गुणनफल, बिना किसी कारक का गुणनफल, गुणात्मक पहचान के बराबर है।

• शून्य वस्तुओं का बिल्कुल एक क्रमचय है: क्रमचय करने के लिए कुछ भी न होने पर, कुछ भी नहीं करना ही एकमात्र पुनर्व्यवस्था है।

• यह परिपाटी क्रमचय-संचय में कई पहचानों को उनके मापदंडों के सभी वैध विकल्पों के लिए वैध बनाती है। उदाहरण के लिए, $n$ के एक सेट से सभी $n$ तत्वों को चुनने के तरीकों की संख्या ${\textstyle {\tbinom {n}{n}}={\tfrac {n!}{n!0!}}=1,}$ एक द्विपद गुणांक पहचान है जो केवल with $0!=1$ के साथ वैध होगी।

• $0!=1$ के साथ, क्रमगुणित के लिए पुनरावृत्ति संबंध $n=1$ पर वैध रहता है। इसलिए, इस परिपाटी के साथ, क्रमगुणित की पुनरावर्ती गणना के लिए आधार मामले के रूप में केवल शून्य का मान होना चाहिए, जिससे गणना सरल हो जाएगी और अतिरिक्त विशेष मामलों की आवश्यकता नहीं होगी।

• $0!=1$ सेट करने से कई सूत्रों, जैसे कि घातांकीय फलन, को घात श्रेणी के रूप में संक्षिप्त रूप से व्यक्त करने की अनुमति मिलती है: ${\textstyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$

• यह विकल्प गामा फलन $0!=\Gamma (0+1)=1$, से मेल खाता है और गामा फलन का सतत फलन होने के लिए यह मान होना चाहिए।

गुण

विकास और सन्निकटन

फैक्टोरियल, स्टर्लिंग सन्निकटन और सरल सन्निकटन $(n/e)^{n}$ की दोहरे लघुगणकीय पैमाने पर तुलना

सापेक्ष त्रुटि एक संक्षिप्त स्टर्लिंग श्रृंखला बनाम पदों की संख्या में

मुख्य लेख: स्टर्लिंग का सन्निकटन

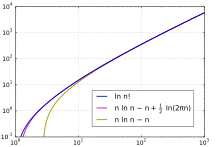
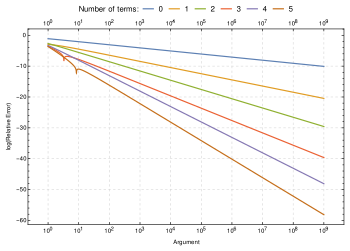
$n$ के एक फलन के रूप में, क्रमगुणित घातीय वृद्धि की तुलना में तेज़ है, लेकिन डबल एक्सपोनेंशियल फ़ंक्शन की तुलना में अधिक धीरे-धीरे बढ़ता है। इसकी वृद्धि दर $n^{n}$ के समान है, लेकिन एक घातांकीय कारक द्वारा धीमी है। इस परिणाम तक पहुँचने का एक तरीका क्रमगुणित का प्राकृतिक लघुगणक लेना है, जो इसके उत्पाद सूत्र को योग में बदल देता है, और फिर एक समाकल द्वारा योग का अनुमान लगाता है:

$$\ln n!=\sum _{x=1}^{n}\ln x\approx \int _{1}^{n}\ln x\,dx=n\ln n-n+1.$$

परिणाम को घातांकित करना (और नगण्य $+1$ पद को अनदेखा करना) $n!$ को $(n/e)^{n}$ के रूप में सन्निकट करता है।}} More carefully bounding the sum both above and below by an integral, using the trapezoid rule, shows that this estimate needs a correction factor proportional to ${\sqrt {n}}$. The constant of proportionality for this correction can be found from the Wallis product, which expresses $\pi$ as a limiting ratio of factorials and powers of two. The result of these corrections is Stirling's approximation:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\,.$$

यहाँ, $\sim$ प्रतीक का अर्थ है कि, जैसे-जैसे $n$ अनंत की ओर जाता है, बाएँ और दाएँ पक्षों के बीच का अनुपात सीमा में एक के करीब पहुँचता है। स्टर्लिंग का सूत्र असिमोटॉटिक श्रृंखला में पहला पद प्रदान करता है जो अधिक संख्या में पदों के लिए ले जाने पर और भी अधिक सटीक हो जाता है:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \right).$$

एक वैकल्पिक संस्करण सुधार पदों में केवल विषम घातांक का उपयोग करता है:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n}}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}}+\cdots \right).$$

इन सूत्रों के कई अन्य रूप भी श्रीनिवास रामानुजन, बिल गोस्पर, और अन्य द्वारा विकसित किए गए हैं।

The binary logarithm of the factorial, used to analyze comparison sorting, can be very accurately estimated using Stirling's approximation. In the formula below, the $O(1)$ term invokes big O notation.

$$\log _{2}n!=n\log _{2}n-(\log _{2}e)n+{\frac {1}{2}}\log _{2}n+O(1).$$

विभाज्यता और अंक

मुख्य लेख: लेजेंड्रे का सूत्र

The product formula for the factorial implies that $n!$ is divisible by all prime numbers that are at most $n$, and by no larger prime numbers. More precise information about its divisibility is given by Legendre's formula, which gives the exponent of each prime $p$ in the prime factorization of $n!$ as

$$\sum _{i=1}^{\infty }\left\lfloor {\frac {n}{p^{i}}}\right\rfloor ={\frac {n-s_{p}(n)}{p-1}}.$$

Here $s_{p}(n)$ denotes the sum of the base-$p$ digits of $n$, and the exponent given by this formula can also be interpreted in advanced mathematics as the p-adic valuation of the factorial. Applying Legendre's formula to the product formula for binomial coefficients produces Kummer's theorem, a similar result on the exponent of each prime in the factorization of a binomial coefficient. Grouping the prime factors of the factorial into prime powers in different ways produces the multiplicative partitions of factorials.

The special case of Legendre's formula for $p=5$ gives the number of trailing zeros in the decimal representation of the factorials. According to this formula, the number of zeros can be obtained by subtracting the base-5 digits of $n$ from $n$, and dividing the result by four. Legendre's formula implies that the exponent of the prime $p=2$ is always larger than the exponent for $p=5$, so each factor of five can be paired with a factor of two to produce one of these trailing zeros. The leading digits of the factorials are distributed according to Benford's law. Every sequence of digits, in any base, is the sequence of initial digits of some factorial number in that base.

Another result on divisibility of factorials, Wilson's theorem, states that $(n-1)!+1$ is divisible by $n$ if and only if $n$ is a prime number. For any given integer $x$, the Kempner function of $x$ is given by the smallest $n$ for which $x$ divides $n!$. For almost all numbers (all but a subset of exceptions with asymptotic density zero), it coincides with the largest prime factor of $x$.

The product of two factorials, $m!\cdot n!$, always evenly divides $(m+n)!$. There are infinitely many factorials that equal the product of other factorials: if $n$ is itself any product of factorials, then $n!$ equals that same product multiplied by one more factorial, $(n-1)!$. The only known examples of factorials that are products of other factorials but are not of this "trivial" form are $9!=7!\cdot 3!\cdot 3!\cdot 2!$, $10!=7!\cdot 6!=7!\cdot 5!\cdot 3!$, and $16!=14!\cdot 5!\cdot 2!$. It would follow from the abc conjecture that there are only finitely many nontrivial examples.

The greatest common divisor of the values of a primitive polynomial of degree $d$ over the integers evenly divides $d!$.

निरंतर प्रक्षेप और गैर-पूर्णांक सामान्यीकरण

गामा फलन (क्रमगुणित से मिलान करने के लिए एक इकाई बाईं ओर स्थानांतरित) क्रमगुणित को गैर-पूर्णांक मानों में लगातार प्रक्षेपित करता है

जटिल गामा फलन के निरपेक्ष मान, गैर-धनात्मक पूर्णांकों पर ध्रुवों को दर्शाते हुए

मुख्य लेख: गामा फलन

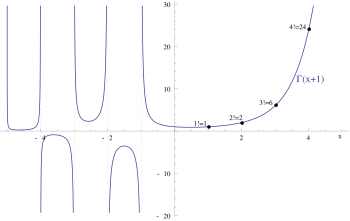
There are infinitely many ways to extend the factorials to a continuous function. The most widely used of these uses the gamma function, which can be defined for positive real numbers as the integral

$$\Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx.$$

The resulting function is related to the factorial of a non-negative integer $n$ by the equation

$$n!=\Gamma (n+1),$$

which can be used as a definition of the factorial for non-integer arguments. At all values $x$ for which both $\Gamma (x)$ and $\Gamma (x-1)$ are defined, the gamma function obeys the functional equation

$$\Gamma (n)=(n-1)\Gamma (n-1),$$

generalizing the recurrence relation for the factorials.

The same integral converges more generally for any complex number $z$ whose real part is positive. It can be extended to the non-integer points in the rest of the complex plane by solving for Euler's reflection formula

$$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}.$$

However, this formula cannot be used at integers because, for them, the $\sin \pi z$ term would produce a division by zero. The result of this extension process is an analytic function, the analytic continuation of the integral formula for the gamma function. It has a nonzero value at all complex numbers, except for the non-positive integers where it has simple poles. Correspondingly, this provides a definition for the factorial at all complex numbers other than the negative integers. One property of the gamma function, distinguishing it from other continuous interpolations of the factorials, is given by the Bohr–Mollerup theorem, which states that the gamma function (offset by one) is the only log-convex function on the positive real numbers that interpolates the factorials and obeys the same functional equation. A related uniqueness theorem of Helmut Wielandt states that the complex gamma function and its scalar multiples are the only holomorphic functions on the positive complex half-plane that obey the functional equation and remain bounded for complex numbers with real part between 1 and 2.

Other complex functions that interpolate the factorial values include Hadamard's gamma function, which is an entire function over all the complex numbers, including the non-positive integers. In the p-adic numbers, it is not possible to continuously interpolate the factorial function directly, because the factorials of large integers (a dense subset of the p-adics) converge to zero according to Legendre's formula, forcing any continuous function that is close to their values to be zero everywhere. Instead, the p-adic gamma function provides a continuous interpolation of a modified form of the factorial, omitting the factors in the factorial that are divisible by p.

The digamma function is the logarithmic derivative of the gamma function. Just as the gamma function provides a continuous interpolation of the factorials, offset by one, the digamma function provides a continuous interpolation of the harmonic numbers, offset by the Euler–Mascheroni constant.

Computation

TI SR-50A, a 1975 calculator with a factorial key (third row, center right)

The factorial function is a common feature in scientific calculators. It is also included in scientific programming libraries such as the Python mathematical functions module and the Boost C++ library. If efficiency is not a concern, computing factorials is trivial: just successively multiply a variable initialized to $1$ by the integers up to $n$. The simplicity of this computation makes it a common example in the use of different computer programming styles and methods.

The computation of $n!$ can be expressed in pseudocode using iteration as

define factorial(n):
  f := 1
  for i := 1, 2, 3, ..., n:
    f := f * i
  return f

or using recursion based on its recurrence relation as

define factorial(n):
  if (n = 0) return 1
  return n * factorial(n − 1)

Other methods suitable for its computation include memoization, dynamic programming, and functional programming. The computational complexity of these algorithms may be analyzed using the unit-cost random-access machine model of computation, in which each arithmetic operation takes constant time and each number uses a constant amount of storage space. In this model, these methods can compute $n!$ in time $O(n)$, and the iterative version uses space $O(1)$. Unless optimized for tail recursion, the recursive version takes linear space to store its call stack. However, this model of computation is only suitable when $n$ is small enough to allow $n!$ to fit into a machine word. The values 12! and 20! are the largest factorials that can be stored in, respectively, the 32-bit and 64-bit integers. Floating point can represent larger factorials, but approximately rather than exactly, and will still overflow for factorials larger than $170!$.

The exact computation of larger factorials involves arbitrary-precision arithmetic, because of fast growth and integer overflow. Time of computation can be analyzed as a function of the number of digits or bits in the result. By Stirling's formula, $n!$ has $b=O(n\log n)$ bits. The Schönhage–Strassen algorithm can produce a $b$-bit product in time $O(b\log b\log \log b)$, and faster multiplication algorithms taking time $O(b\log b)$ are known. However, computing the factorial involves repeated products, rather than a single multiplication, so these time bounds do not apply directly. In this setting, computing $n!$ by multiplying the numbers from 1 to $n$ in sequence is inefficient, because it involves $n$ multiplications, a constant fraction of which take time $O(n\log ^{2}n)$ each, giving total time $O(n^{2}\log ^{2}n)$. A better approach is to perform the multiplications as a divide-and-conquer algorithm that multiplies a sequence of $i$ numbers by splitting it into two subsequences of $i/2$ numbers, multiplies each subsequence, and combines the results with one last multiplication. This approach to the factorial takes total time $O(n\log ^{3}n)$: one logarithm comes from the number of bits in the factorial, a second comes from the multiplication algorithm, and a third comes from the divide and conquer.

Even better efficiency is obtained by computing n! from its prime factorization, based on the principle that exponentiation by squaring is faster than expanding an exponent into a product. An algorithm for this by Arnold Schönhage begins by finding the list of the primes up to $n$, for instance using the sieve of Eratosthenes, and uses Legendre's formula to compute the exponent for each prime. Then it computes the product of the prime powers with these exponents, using a recursive algorithm, as follows:

• Use divide and conquer to compute the product of the primes whose exponents are odd
• Divide all of the exponents by two (rounding down to an integer), recursively compute the product of the prime powers with these smaller exponents, and square the result
• Multiply together the results of the two previous steps

The product of all primes up to $n$ is an $O(n)$-bit number, by the prime number theorem, so the time for the first step is $O(n\log ^{2}n)$, with one logarithm coming from the divide and conquer and another coming from the multiplication algorithm. In the recursive calls to the algorithm, the prime number theorem can again be invoked to prove that the numbers of bits in the corresponding products decrease by a constant factor at each level of recursion, so the total time for these steps at all levels of recursion adds in a geometric series to $O(n\log ^{2}n)$. The time for the squaring in the second step and the multiplication in the third step are again $O(n\log ^{2}n)$, because each is a single multiplication of a number with $O(n\log n)$ bits. Again, at each level of recursion the numbers involved have a constant fraction as many bits (because otherwise repeatedly squaring them would produce too large a final result) so again the amounts of time for these steps in the recursive calls add in a geometric series to $O(n\log ^{2}n)$. Consequentially, the whole algorithm takes time $O(n\log ^{2}n)$, proportional to a single multiplication with the same number of bits in its result.

इन्हें भी देखें

• गामा फलन
• क्रमचय-संचय

बाहरी कड़ियाँ

• सन्निकटन सूत्र
• क्रमगुणित नोटेशन n! के बारे में सब कुछ
• "डबल क्रमगुणित व्युत्पन्न"

क्रमगुणित कैलकुलेटर और एल्गोरिदम

• क्रमगुणित कैलकुलेटर: तुरन्त 10^14! तक के क्रमगुणित ढूंढता है
• एनिमेटेड क्रमगुणित कैलकुलेटर: सामान्य प्राथमिक विद्यालय के एग्लॉरिथम का उपयोग करके हाथ से गणना किए गए क्रमगुणित को दर्शाता है
• "क्रमगुणित" एड पेग, जूनियर और रॉब मॉरिस द्वारा, वोल्फ्राम डेमोंस्ट्रेशन प्रोजेक्ट, 2007.
• तेज़ क्रमगुणित फलन (जावा, सी#, सी++, स्काला और गो में स्रोत कोड के साथ)