चुंबकत्व

यह सुझाव दिया जाता है कि इस लेख या भाग का चुम्बकत्व के साथ विलय कर दिया जाए। (वार्ता)

चुंबकत्व प्रायोगिक चुंबकीय क्षेत्र के परमाणु या उप-परमाणु स्तर पर प्रतिक्रिया करने वाले तत्वों का गुण है। उदाहरण के लिए, चुंबकत्व का ज्ञात रूप है जो की लौह चुंबकत्व है, जहां कुछ लौह-चुंबकीय तत्व स्वयं अपना निरंतर चुंबकीय क्षेत्र उत्पन्न करते रहते हैं। हालांकि, सभी तत्व चुंबकीय क्षेत्र की उपस्थिति से कम या अधिक स्तर तक प्रभावित होते हैं। कुछ चुंबकीय क्षेत्र (अणुचंबकत्व) के प्रति आकर्षित होते हैं; अन्य चुंबकीय क्षेत्र (प्रति-चुंबकत्व) से विकर्षित होते हैं; जब कि दूसरों का प्रायोगिक चुंबकीय क्षेत्र के साथ और अधिक जटिल संबंध होता है। पदार्थ है कि चुंबकीय क्षेत्रों द्वारा नगण्य रूप से प्रभावित पदार्थ ग़ैर-चुंबकीय पदार्थ के रूप में जाने जाते हैं। इनमें शामिल हैं तांबा, एल्यूमिनियम, गैस और प्लास्टिक....

सामग्री की चुंबकीय स्थिति (या चरण) तापमान (और दबाव तथा प्रायोगिक चुंबकीय क्षेत्र जैसे परिवर्तनशील तत्वों) पर निर्भर करता है ताकि अपने तापमान आदि के आधार पर सामग्री चुंबकत्व के एक से अधिक रूप प्रदर्शित कर सके।

इतिहास[संपादित करें]

वैशेषिक नामक ग्रन्थ में ( ५-१-१५ ) ऋषि कणाद लिखते हैं कि चुम्बक की अदृश्य कर्षण शक्ति के कारण लोहा चुम्बक के प्रति खींचा जाता है ।^[1] अरस्तू लगभग ई.पू. 625 से ई.पू. 545 के बीच जीवित थेल्स को चुंबकत्व पर प्रथम वैज्ञानिक चर्चा कहला सकने का श्रेय देते हैं।^[2] लगभग इसी समय प्राचीन भारत में, भारतीय शल्य-चिकित्सक सुश्रुत ने शल्य-चिकित्सा के लिए चुंबक का सर्वप्रथम उपयोग किया।^[3]

प्राचीन चीन में चुंबकत्व पर उपलब्ध प्रारंभिक साहित्यिक सन्दर्भ ई.पू. चौथी सदी में बुक ऑफ़ डेविल वैली मास्टर (鬼谷子) नामक पुस्तक में मिलता है: "चुंबक-पत्थर लोहे को पास बुलाता है या आकर्षित करता है।"^[4] सुई को आकर्षित करने का प्रारंभिक उल्लेख ईस्वी सन् 20 और 100 के बीच लिखी गई कृति में मिलता है (लोइन-हेन्ग): "एक चुंबक-पत्थर सुई को आकर्षित करता है।"^[5] प्राचीन चीनी वैज्ञानिक शेन कुओ (1031-1095) पहले व्यक्ति थे जिन्होंने चुंबकीय सुई दिक्सूचक के बारे में लिखा और यह कि वास्तविक उत्तर की खगोलीय अवधारणा को लागू करते हुए मार्गनिर्देशन की सटीकता को उसने सुधारा (ड्रीम पूल एसेज़, ईस्वी सन् 1088) और ऐसा ज्ञात होता है कि 12 वीं सदी तक चीनी द्वारा मार्गनिर्देशन के लिए चुंबक-पत्थर दिक्सूचक का उपयोग किया जाने लगा था।

यूरोप में 1187 तक अलेक्जेंडर नेखम पहले व्यक्ति थे जिन्होंने दिक्सूचक और मार्गनिर्देशन के लिए उसके उपयोग को वर्णित किया। 1269 में पीटर पेरेग्रिनस डे मेरीकोर्ट ने एपिस्टोला डे मैगनेट लिखा, जो चुंबक के गुणों को वर्णित करने वाला प्रथम वर्तमान ग्रंथ है। 1282 में, चुंबक के गुण और शुष्क दिक्सूचक की चर्चा येमेनी भौतिक विज्ञानी, खगोल विज्ञानी और भूगोलवेत्ता अल-अशरफ़ ने की। ^[6]

1600 में, विलियम गिलबर्ट ने (चुंबक तथा चुंबकीय पिंड और महान चुंबक पृथ्वी पर) अपना De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure प्रकाशित किया। इस पुस्तक में वे टेरेला कहे जाने वाले अपने पृथ्वी के मॉडल के साथ किए गए अपने प्रयोगों का वर्णन किया है। उनके प्रयोगों से उन्होंने निष्कर्ष निकाला कि स्वयं पृथ्वी चुंबकीय है और यही कारण है कि दिक्सूचक उत्तर की ओर इंगित करते हैं (पहले, कुछ का मानना था कि ध्रुवतारा (पोलारिस) या उत्तरी ध्रुव पर कोई बड़ा चुंबकीय द्वीप है जो दिक्सूचक को आकर्षित करता है).

बिजली और चुंबकत्व के बीच रिश्ते की समझ 1819 में कोपेनहेगन विश्वविद्यालय के प्रोफ़ेसर हैन्स क्रिश्चियन ओर्स्टेड के कार्य के साथ शुरू हुआ, जिन्होंने कमोबेश आकस्मिक घटना से खोजा कि विद्युत तरंग दिक्सूचक की सुई को प्रभावित कर सकती है। यह ऐतिहासिक प्रयोग ओर्स्टेड प्रयोग के रूप में जाना जाता है। एंड्रे-मेरी एम्पियर, कार्ल फ्रेडरिच गॉस, माइकल फ़राडे और अन्य द्वारा चुंबकत्व तथा विद्युत के बीच और संबंधों की खोज के साथ, कई अन्य प्रयोगों ने इनका अनुवर्तन किया। जेम्स क्लर्क मैक्सवेल ने मैक्सवेल समीकरण, विद्युत-चुंबकत्व के क्षेत्र में विद्युत, चुंबकत्व और प्रकाशिकी के एकीकरण द्वारा इन अंतर्दृष्टियों को संश्लेषित और विस्तृत किया। 1905 में, आइंस्टीन ने अपने विशेष सापेक्षता के सिद्धांत के प्रवर्तन के लिए इन सिद्धांतों का उपयोग किया,^[7] इस अपेक्षा सहित कि सभी जड़ सन्दर्भ ढांचों में सिद्धांत सटीक बैठते हैं।

गॉज़ सिद्धांत, क्वांटम विद्युत गतिकी, विद्युत दुर्बलता सिद्धांत और अंततः मानक नमूने के अधिक मौलिक सिद्धांतों में संयोजन द्वारा विद्युत-चुंबकत्व का विकास 21 वीं सदी में जारी रहा।

चुंबकत्व के स्रोत[संपादित करें]

आइंस्टीन-डे हास प्रभाव "चुंबकन द्वारा घूर्णन" और उसके व्युत्क्रम में बार्नेट प्रभाव या "घूर्णन द्वारा चुंबकत्व" में स्थूल पैमाने पर कोणीय संवेग और चुंबकत्व के बीच बहुत निकट का संबंध मौजूद है।^[8]

परमाणु और उप-परमाणु पैमाने पर, यह संबंध घूर्ण चुंबकीय अनुपात, कोणीय संवेग के प्रति चुंबकीय आघूर्ण के अनुपात द्वारा व्यक्त होता है।

चुंबकत्व का मूल दो स्रोतों से उभरता है:

विद्युत तरंग या अधिक सामान्यतः, गतिशील विद्युत आवेश चुंबकीय क्षेत्र उत्पन्न करते हैं (देखें मैक्सवेल समीकरण).
कई कणों में अशून्य "नैज" (या "प्रचक्रण") चुंबकीय आघूर्ण होते हैं। वैसे ही जैसे प्रत्येक कण में, सहज रूप से, एक निश्चित द्रव्यमान और आवेश होता है, प्रत्येक में निश्चित चुंबकीय आघूर्ण होता है, जो संभवतः शून्य हो सकता है।

चुंबकीय सामग्रियों में, चुंबकत्व के स्रोत नाभिक के आस-पास इलेक्ट्रॉन की कक्षीय कोणीय गति और इलेक्ट्रॉनों के आंतरिक चुंबकीय संवेग होते हैं (देखें इलेक्ट्रॉन चुंबकीय द्विध्रुवीय संवेग). चुंबकत्व के अन्य स्रोत हैं नाभिक के परमाणु चुंबकीय संवेग जो आम तौर पर इलेक्ट्रॉन चुंबकीय संवेगों से कई हज़ार गुणा छोटे होते हैं, अतः वे तत्वों के चुंबकन के सन्दर्भ में नगण्य हैं। नाभिक चुंबकीय संवेग अन्य सन्दर्भों में महत्वपूर्ण हैं, विशेषकर परमाणु चुंबकीय अनुनाद (NMR) और चुंबकीय अनुनाद प्रतिबिंबन (MRI).

आम तौर पर, किसी द्रव्य में इलेक्ट्रॉनों की भारी संख्या इस प्रकार व्यवस्थित होती है कि उनके चुंबकीय संवेग (कक्षीय और आंतरिक दोनों) रद्द हो जाते हैं। यह कुछ हद तक इलेक्ट्रॉनों का पाउली अपवर्जन सिद्धांत (देखें इलेक्ट्रॉन विन्यास) के परिणामस्वरूप विपरीत आंतरिक चुंबकीय संवेगों के साथ युग्मों में संयोजित होना, या शून्य निवल कक्षीय गति के साथ पूरित उपकोशों के साथ संयोजन. दोनों ही मामलों में, इलेक्ट्रॉन व्यवस्था प्रत्येक इलेक्ट्रॉन से चुंबकीय संवेगों को बिलकुल रद्द करने के लिए है। इसके अलावा, जब इलेक्ट्रॉन विन्यास ऐसा है कि अयुग्मित इलेक्ट्रॉन और/या अपूरित उपकोश मौजूद हैं, बहुधा ऐसा मामला होता है कि ठोस में विविध इलेक्ट्रॉन चुंबकीय संवेगों में योगदान देते हैं जो अलग, यादृच्छिक दिशाओं में इंगित होते हैं, जिससे सामग्री चुंबकीय नहीं होती है।

लेकिन, कभी कभी - या तो अनायास या प्रयुक्त बाहरी चुंबकीय क्षेत्र के कारण - प्रत्येक इलेक्ट्रॉन चुंबकीय संवेग, औसतन, व्यवस्थित हो जाते हैं। इसके बाद द्रव्य निवल कुल चुंबकीय क्षेत्र उत्पन्न कर सकता है, जो संभवतः काफी मजबूत हो सकता है।

द्रव्य का चुंबकीय व्यवहार उसकी संरचना, विशेषकर उपरोक्त कारणों से इलेक्ट्रॉन विन्यास और साथ ही तापमान पर निर्भर करता है। उच्च तापमान पर, यादृच्छिक तापीय संवेग इलेक्ट्रॉन के लिए संरेखण का अनुरक्षण अधिक जटिल बना देता है।

विषय[संपादित करें]

चुंबकत्व के प्रकार के अनुक्रम. देखें मायर्स.^[9]

प्रति-चुंबकत्व[संपादित करें]

प्रति-चुंबकत्व सभी द्रव्यों में प्रकट होता है और प्रयुक्त चुंबकीय क्षेत्र का विरोध करना तत्वों की प्रवृत्ति है और इसलिए, चुंबकीय क्षेत्र द्वारा विकर्षित होना है। हालांकि, अणुचुंबकीय गुणों वाले द्रव्य में (अर्थात्, बाह्य चुंबकीय क्षेत्र को बढ़ाने की प्रवृत्ति सहित), अणुचुंबकीय व्यवहार हावी होता है।^[10] इस प्रकार, अपने सार्वभौमिक उपस्थिति के बावजूद, प्रति-चुंबकीय व्यवहार केवल विशुद्ध प्रति-चुंबकीय द्रव्य में देखा जाता है। किसी प्रति-चुंबकीय द्रव्य में, कोई अयुग्मित इलेक्ट्रॉन नहीं होते हैं, अतः आंतरिक इलेक्ट्रॉन चुंबकीय संवेग कोई थोक प्रभाव उत्पन्न नहीं कर सकते हैं। इन मामलों में, चुंबकत्व इलेक्ट्रॉन के कक्षीय संवेगों से उभरता है, जिसे शास्त्रीय तौर पर निम्नतः समझा जा सकता है:

जब किसी द्रव्य को चुंबकीय क्षेत्र में रखा जाता है, नाभिक का चक्कर लगाने वाले इलेक्ट्रॉनों द्वारा नाभिक के प्रति कूलंब आकर्षण के अतिरिक्त, चुंबकीय क्षेत्र से लॉरेंज़ शक्ति का अनुभव किया जाएगा. इलेक्ट्रॉन की परिक्रमा की दिशा पर निर्भर करते हुए, यह बल उन्हें नाभिक की ओर खींचते हुए, इलेक्ट्रॉनों के केन्द्राभिमुख बल को बढ़ा सकता है या नाभिक से दूर खींचते हुए बल को कम कर सकता है। यह प्रभाव क्रमिक रूप से कक्षीय चुंबकीय संवेगों को बढ़ाता है जो क्षेत्र के विपरीत सुयोजित थे और क्षेत्र के समानांतर सुयोजित संवेगों को कम करता है (लेन्ज़ सिद्धांत के अनुसार). यह प्रयुक्त क्षेत्र की विपरीत दिशा में छोटे थोक चुंबकीय संवेग में परिणत होता है।

कृपया ध्यान दें कि यह विवरण केवल स्वतःशोध के रूप में है; उचित समझ के लिए क्वांटम-यांत्रिक विवरण की आवश्यकता है।

ध्यान दें कि सभी द्रव्यों को इस कक्षीय प्रतिक्रिया से गुजरना पड़ता है। तथापि, अणुचुंबकीय और लौह चुंबकीय पदार्थों में, प्रति-चुंबकत्व प्रभाव अयुग्मित इलेक्ट्रॉनों के बहुत मजबूत प्रभाव से अभिभूत हैं।

अणु-चुंबकत्व[संपादित करें]

अणुचुंबकीय द्रव्य में अयुग्मित इलेक्ट्रॉन मौजूद होते हैं, अर्थात् परमाणु या आणविक कक्षीय, जिनमें केवल एक इलेक्ट्रॉन होता है। जबकि पाउली अपवर्जन सिद्धांत के अनुसार युग्मित इलेक्ट्रॉनों के लिए ज़रूरी है कि उनके आंतरिक ('प्रचक्रण') चुंबकीय संवेग विपरीत दिशाओं में इंगित हों, जो उनके चुंबकीय क्षेत्रों को रद्द कर दें, एक अयुग्मित इलेक्ट्रॉन अपने चुंबकीय संवेग को किसी भी दिशा में संरेखित करने के लिए स्वतंत्र है। जब एक बाह्य चुंबकीय क्षेत्र प्रयुक्त होता है, ये चुंबकीय संवेग खुद को प्रयुक्त क्षेत्र की दिशा के अनुरूप संरेखित करते हैं, जिससे वे प्रबलित होते हैं।

लौह-चुंबकत्व[संपादित करें]

अणु-चुंबकीय द्रव्य के अनुसार लौह-चुंबक में अयुग्मित इलेक्ट्रॉन होते हैं। तथापि, इलेक्ट्रॉनों के चुंबकीय संवेगों की किसी प्रयुक्त क्षेत्र के समानांतर रहने की प्रवृत्ति के अलावा, इन द्रव्यों में न्यून ऊर्जा स्थिति के अनुरक्षण के लिए एक दूसरे के समानांतर इन चुंबकीय संवेगों के विन्यस्त होने की प्रवृत्ति भी होती है। इस प्रकार, जब प्रयुक्त क्षेत्र हटा भी दें, द्रव्य में इलेक्ट्रॉन एक समानांतर अभिविन्यास बनाए रखते हैं।

प्रत्येक लौह-चुंबकीय पदार्थ का अपना व्यक्तिगत तापमान होता है, जो क्यूरी तापमान या क्यूरी बिंदु कहलाता है, जिससे ऊपर वह अपने लौह-चुंबकीय गुणों को खो देता है। इसका कारण है विकार की तापीय प्रवृत्ति लौह-चुंबकीय क्रम के कारण ऊर्जा-न्यूनीकरण को दबा देती है।

कुछ जाने-माने लौह-चुंबकीय द्रव्य जो (चुंबक बनाने के लिए) आसानी से पहचाने जाने वाले चुंबकीय गुणों को प्रदर्शित करते हैं, वे हैं निकल, लोहा, कोबाल्ट, गैडोलिनियम और उनके मिश्र धातु.

चुंबकीय डोमेन[संपादित करें]

किसी लौह-चुंबकीय द्रव्य में परमाणुओं के चुंबकीय संवेग उन्हें छोटे स्थाई चुंबकों की भांति व्यवहार करने के लिए बाध्य करते हैं। वे एक साथ जुड़े रहते हैं और चुंबकीय डोमेन या वेइस डोमेन कहलाने वाले कमोबेश एकरूप संरेखन वाले छोटे क्षेत्रों में संरेखित कर लेते हैं। चुंबकीय डोमेन को, चित्र में सफ़ेद रेखाओं के समान दिखने वाली चुंबकीय डोमेन सीमाओं को प्रकट करने के लिए एक चुंबकीय बल सूक्ष्मदर्शी के माध्यम से देखा जा सकता है। कई वैज्ञानिक प्रयोग मौजूद हैं जोकि भौतिक रूप से चुंबकीय क्षेत्र दिखा सकते हैं।

जब डोमेन में कई अणु होते हैं, वह अस्थिर हो जाता है और दो विपरीत दिशाओं में सुयोजित डोमेनों में संरेखित हो जाता है ताकि वे दाईं और दिखाए गए अनुसार अधिक स्थिरता के साथ एक दूसरे से जुड़े रहें.

जब चुंबकीय क्षेत्र के संपर्क में हों, डोमेन सीमाएं गतिशील होती हैं ताकि चुंबकीय क्षेत्र से संरेखित डोमेनों में वृद्धि हो और बाईं ओर दिखाए गए अनुसार संरचना पर हावी हो सकें. जब चुंबकन क्षेत्र हटा दिया जाए, तो संभवतः डोमेन अचुंबकीय दशा में वापस न लौटें. इसके परिणामस्वरूप लौह-चुंबकीय द्रव्य चुंबकीय हो जाता है, जिससे स्थाई चुंबक बन जाता है।

जब पर्याप्त दृढ़ता से चुंबकीय हो जाता है ताकि मौजूदा डोमेन बाक़ी सभी को केवल एक एकल डोमेन में समेट दें, तब द्रव्य चुंबकीय रूप से संतृप्त हो जाता है। जब चुंबकीय लौह-चुंबकत्व द्रव्य को क्यूरी बिंदु तापमान तक गरम किया जाता है, तो अणुओं में उस बिंदु तक हलचल मच जाती है कि चुंबकीय डोमेन का संगठन बिखर जाता है और उनके द्वारा व्युत्पन्न चुंबकीय गुण ख़त्म हो जाते हैं। जब द्रव्य को ठंडा किया जाता है, इस डोमेन की संरेखण संरचना अनायास इस प्रकार लौट आती है जैसे द्रव क्रिस्टलीय ठोस में जम जाता है।

प्रति-लौहचुंबकत्व[संपादित करें]

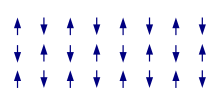
लौहचुंबकत्व से उलटे प्रति-लौहचुंबकत्व में विपरीत दिशाओं में सूचित करने के लिए आस-पास के कर्षणशक्ति वाले इलेक्ट्रॉनों में आंतरिक चुंबकीय संवेग की प्रवृत्ति होती है। जब सभी परमाणु, पदार्थ में व्यवस्थित होते हैं ताकि प्रत्येक पड़ोसी 'प्रति-संरेखित' हों, पदार्थ प्रति-लौहचुंबकीय होता है। प्रति-लौहचुंबकों में शून्य निवल चुंबकीय संवेग होता है, जिसका अर्थ है उनके द्वारा कोई क्षेत्र निर्मित नहीं होता है। प्रति-लौहचुंबक अन्य प्रकार के व्यवहारों की तुलना में कम सामान्य हैं और ज्यादातर कम तापमान पर देखे जा सकते हैं। अलग-अलग तापमानों में, प्रति-लौहचुंबकों द्वारा प्रति-चुंबकीय और लौह-चुंबकीय गुणों को प्रदर्शित करते हुए देखा जा सकता है।

कुछ द्रव्यों में, पड़ोसी इलेक्ट्रॉन विपरीत दिशाओं में इंगित करना चाहते हैं, लेकिन वहां कोई ज्यामितीय व्यवस्था नहीं होती जिनमें प्रत्येक पड़ोसी युग्म प्रति-संरेखित हो। इसे स्पिन ग्लास कहा जाता है और यह ज्यामितीय हताशा का एक उदाहरण है।

लौह-चुंबकत्व[संपादित करें]

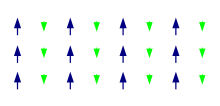
लौह-चुंबकत्व के समान, क्षेत्र की अनुपस्थिति में लौहचुंबक अपना चुंबकत्व बनाए रखते हैं। तथापि, प्रति-लौहचुंबकों की भांति, इलेक्ट्रॉन प्रचक्रणों के पड़ोसी युग्म विपरीत दिशाओं में इंगित करते हैं। ये दो गुण विरोधाभासी नहीं हैं, क्योंकि इष्टतम ज्यामितीय व्यवस्था में, विरोधी दिशा में इंगित करने वाले उपजालकों की तुलना में, एक दिशा में इंगित करने वाले उपजालक इलेक्ट्रॉनों से अधिक चुंबकीय संवेग रहता है।

पहले खोजा गया चुंबकीय पदार्थ मैग्नेटाइट, मूलतः लौह-चुंबक माना गया था; तथापि लौह-चुंबकत्व की खोज के साथ, लुई नील ने इसे ग़लत साबित किया।

सुपर-प्रतिचुंबकत्व[संपादित करें]

जब लौह-चुंबक पर्याप्त छोटा होता है, वह ब्राउनियन संवेग के अधीन एकल चुंबकीय प्रचक्रण के समान कार्य करता है। चुंबकीय क्षेत्र के प्रति इसकी प्रतिक्रिया गुणात्मक रूप से प्रतिचुंबक के समान ही, लेकिन बहुत बड़ी होती है।

विद्युत-चुंबकत्व[संपादित करें]

विद्युत-चुंबक एक ऐसा चुंबक है जिसका चुंबकत्व विद्युत धारा के प्रवाह से उत्पन्न होता है। जब धारा बंद हो जाती है, तो चुंबकीय क्षेत्र गायब हो जाता है।

जब चुंबकीय क्षेत्र पैदा करते हुए विद्युत लागू किया जाए तो विद्युत चुबंक पेपर क्लिप को आकर्षित करते हैं। जब विद्युत और चुंबकीय क्षेत्र को हटा दिया जाए तो विद्युत चुंबक उन्हें खो देता है।

अन्य प्रकार के चुंबकत्व[संपादित करें]

आण्विक चुंबक
मेटा चुंबकत्व
अणु आधारित चुंबक
स्पिन ग्लास

या एक चुंबक.

चुंबकत्व, विद्युत और विशेष सापेक्षता[संपादित करें]

आइंस्टीन की विशेष सापेक्षता सिद्धांत के परिणामस्वरूप, विद्युत और चुंबकत्व मौलिक रूप से आपस में जुड़े हैं। दोनों, विद्युत रहित चुंबकत्व और चुंबकत्व रहित विद्युत, विशेष सापेक्षता के साथ लंबाई संकुचन, समय विस्तार और इस तथ्य के चलते कि चुंबकीय बल वेग आधारित है, जैसे प्रभावों के कारण असंगत हैं। तथापि, जब विद्युत और चुंबकत्व, दोनों को ध्यान में रखा जाता है, परिणामी सिद्धांत (विद्युत-चुंबकत्व) विशेष सापेक्षता के पूरी तरह अनुरूप है।^[7]^[11] विशेष रूप से, जो घटना एक पर्यवेक्षक को विशुद्ध रूप से विद्युतीय लगती है वही दूसरे को विशुद्ध रूप से चुंबकीय लग सकती है, या अधिक सामान्यतः विद्युत और चुंबकत्व के सापेक्ष योगदान सन्दर्भ के ढांचे पर निर्भर करती है। इस प्रकार, विशेष सापेक्षता विद्युत और चुंबकत्व को विद्युत-चुंबकत्व कहलाने वाले एकल, अविभाज्य तत्व में "मिश्रित" करती है, जो सापेक्षता द्वारा अंतरिक्ष और समय को अंतरिक्ष-समय में "मिश्रित" करने के अनुरूप है।

चुंबकीय क्षेत्र और बल[संपादित करें]

काग़ज़ पर लोहे के बुरादे से धारी चुंबक की शक्ति के चुंबकीय लाइनों को दिखाया गया

चुंबकत्व तत्व की "मध्यस्थता" चुंबकीय क्षेत्र द्वारा किया जाता है। विद्युत धारा या चुंबकीय द्विध्रुव चुंबकीय क्षेत्र उत्पन्न करता है और बदले में, वह क्षेत्र, क्षेत्रों में रहने वाले अन्य कणों पर चुंबकीय बल प्रदान करता है।

मैक्सवेल के समीकरण, जो स्थिर धाराओं के मामले में बायोट-सावर्ट सिद्धांत को सरल बनाते हैं, इन बलों को शासित करने वाले क्षेत्रों के मूल और व्यवहार को वर्णित करते हैं। इसलिए जब भी विद्युत आवेशित कण गतिशील होते हैं, चुंबकत्व को देखा जाता है --- उदाहरण के लिए, विद्युत धारा में इलेक्ट्रॉन के संचलन से, या कुछ मामलों में परमाणु के नाभिक के आस-पास इलेक्ट्रॉन की कक्षीय गति से. वे भी क्वांटम-यांत्रिक प्रचक्रण से उभरने वाले "आंतरिक" चुंबकीय द्विध्रुव से उत्पन्न होते हैं।

चुंबकीय क्षेत्र बनाने वाली स्थितियां ही - धारा में या एक परमाणु और आंतरिक चुंबकीय द्विध्रुव में गतिशील आवेश - भी ऐसी स्थितियां हैं जिनमें चुंबकीय क्षेत्र का बल उत्पन्न करते हुए, एक प्रभाव होता है। गतिशील आवेश के लिए सूत्र निम्नतः है; आंतरिक द्विध्रुव पर बलों के लिए, चुंबकीय द्विध्रुव देखें.

जब कोई आवेशित कण चुंबकीय क्षेत्र B के माध्यम से गुज़रता है, वह प्रति उत्पाद द्वारा दिए गए F लॉरेंज़ बल को महसूस करता है:^[12]

\mathbf {F} =q(\mathbf {v} \times \mathbf {B} )

जहां

q

कण का विद्युत आवेश है और

v कण का वेक्टर वेग है

क्योंकि यह प्रति-उत्पाद है, बल कण की गति और चुंबकीय क्षेत्र, दोनों के लंब में है। यह इसका अनुगमन करता है कि चुंबकीय बल कण पर कोई काम नहीं करता; वह कण की गति की दिशा को परिवर्तित कर सकता है, लेकिन उसकी चाल को तेज़ या धीमा नहीं कर सकता. बल का परिमाण है

F=qvB\sin \theta \,

जहां $\theta$ v और B के बीच का कोण है।

गतिशील आवेश के वेग सदिश की दिशा, चुंबकीय क्षेत्र और प्रयुक्त बल को निर्धारित करने के लिए एक उपकरण, आपके दाहिने हाथ की तर्जनी को "V", बीच की उंगली को "B" और अंगूठे को "F" लेबल करना है। जब बंदूक की तरह विन्यास बनाएं, जहां बीच की उंगली तर्जनी को पार करे, उंगलियां क्रमशः वेग सदिश, चुंबकीय क्षेत्र सदिश और बल सदिश का प्रतिनिधित्व करती हैं। दाहिने हाथ का नियम भी देखें.

चुंबकीय द्विध्रुव[संपादित करें]

"दक्षिण ध्रुव" और "उत्तर ध्रुव" शब्दों के साथ, प्रकृति में प्रदर्शित चुंबकीय क्षेत्र का सबसे आम स्रोत है द्विध्रुव, जो दिक्सूचकों के रूप में चुंबकों के उपयोग जितना पुराना है, जहां वे पृथ्वी के चुंबकीय क्षेत्र के साथ परस्पर क्रिया द्वारा विश्व के उत्तर और दक्षिण ध्रुव को सूचित करते थे। चूंकि चुंबक के विपरीत सिरे एक दूसरे के प्रति आकर्षित होते हैं, चुंबक का उत्तरी ध्रुव दूसरे चुंबक के दक्षिणी ध्रुव के प्रति आकर्षित होता है। पृथ्वी का उत्तरी चुंबकीय ध्रुव (संप्रति कनाडा के उत्तर में आर्कटिक महासागर) भौतिक रूप से दक्षिण ध्रुव है, क्योंकि वह दिक्सूचक के उत्तरी ध्रुव को आकर्षित करता है।

चुंबकीय क्षेत्र में ऊर्जा रहती है और भौतिक प्रणालियां कम ऊर्जा वाले विन्यासों की ओर गतिशील होती हैं। जब प्रति-चुंबकीय द्रव्य को चुंबकीय क्षेत्र में रखा जाता है, तो चुंबकीय द्विध्रुव स्वयं को उस क्षेत्र के विपरीत ध्रुवता पर संरेखित करने का प्रयास करता है, जिसके द्वारा निवल क्षेत्र बल कम हो जाता है। जब लौह-चुंबकीय द्रव्य को चुंबकीय क्षेत्र के अंतर्गत रखा जाता है, तब चुंबकीय द्विध्रुव प्रयुक्त क्षेत्र के साथ संरेखित होते हैं, इस प्रकार चुंबकीय डोमेनों की डोमेन दीवारों को विस्तृत करते हैं।

चुंबकीय एकध्रुव[संपादित करें]

चूंकि बार चुंबक को लौहचुंबकत्व समूचे बार में एकसमान रूप से वितरित इलेक्ट्रॉनों के माध्यम से मिलता है, जब बार मैगनेट को दो हिस्सों में काटा जाता है, प्रत्येक टुकड़ा छोटा बार मैगनेट होता है। हालांकि कहा जाता है कि चुंबक में उत्तरी ध्रुव और दक्षिणी ध्रुव होते हैं, इन दो ध्रुवों को एक दूसरे से अलग नहीं किया जा सकता है। एकध्रुव – अगर ऐसा कोई विद्यमान हो – एक नई मौलिक रूप से अलग क़िस्म का चुंबकीय वस्तु होगी। वह अकेले उत्तरी ध्रुव के रूप में कार्य करेगी, जो दक्षिणी ध्रुव से, या इसके विपरीत जुड़ी नहीं होगी। एकध्रुव विद्युत धारा के समान चुंबकीय आवेश वहन करेगा। 1931 के बाद से क्रमिक खोजों के बावजूद, उन्हें कभी नहीं देखा गया,2010 के अनुसार ^[update] और संभवतः वे विद्यमान नहीं होंगे। ^[13]

फिर भी, कुछ सैद्धांतिक भौतिकी नमूने इन चुंबकीय एकध्रुवों के अस्तित्व का पूर्वानुमान लगाते हैं। 1931 में पॉल डिराक ने देखा कि विद्युत और चुंबकत्व में कुछ प्रतिसाम्य होने के कारण, जैसे कि क्वांटम सिद्धांत का पूर्वानुमान है कि व्यक्तिगत धनात्मक या ऋणात्मक आवेश बिना विपरीत आवेश के देखे जा सकते हैं, वियुक्त दक्षिण और उत्तर चुंबकीय ध्रुव परिलक्षित होने चाहिए। क्वांटम सिद्धांत का उपयोग करते हुए डिराक ने प्रदर्शित किया कि यदि चुंबकीय एकध्रुव विद्यमान हैं, तो विद्युत आवेश के क्वांटमीकरण की व्याख्या की जा सकती है-अर्थात् क्यों परिलक्षित तत्वीय कण ऐसे आवेश वहन करते हैं जो इलेक्ट्रॉन के आवेश के गुणज हैं।

कुछ भव्य एकीकृत सिद्धांत तत्वीय कणों के विपरीत, एकध्रुवों का पूर्वानुमान लगाते हैं, जो सॉलिटॉन (स्थानीयकृत ऊर्जा पैकेट) हैं। बिग बैंग में निर्मित एकध्रुवों की संख्या का अनुमान लगाने के लिए इन नमूनों के उपयोग के प्रारंभिक परिणामों ने ब्रह्मांडीय प्रेक्षणों का खंडन किया — एकध्रुव इतने ज़्यादा और अतिविशाल होंगे कि उनका ब्रह्मांड में विस्तार बहुत पहले बंद हो गया होगा। तथापि, मुद्रास्फीति का विचार (जिसके लिए इस समस्या ने आंशिक प्रेरणा के रूप में काम किया) इस समस्या को हल करने में सफल रहा था, जहां नमूने बनाए गए जिनमें एकध्रुव विद्यमान होंगे लेकिन वर्तमान प्रेक्षणों के साथ उनकी अनुरूपता दुर्लभ थी।^[14]

चुंबकत्व का क्वांटम-यांत्रिक मूल[संपादित करें]

सिद्धांततः सभी प्रकार के चुंबकत्व (सुपर-चालकता के समान) विशिष्ट क्वांटम-यांत्रिक तत्व से व्युत्पन्न हुए हैं जिनकी आसानी से व्याख्या नहीं की जा सकती (उदा. क्वांटम यांत्रिकी का गणितीय सूत्रीकरण, विशेष रूप से प्रचक्रण और पाउली सिद्धांत पर अध्याय). वाल्टर हेटलर और फ्रिट्ज लंदन द्वारा 1927 में पहले से ही एक सफल नमूना विकसित किया गया था, जिन्होंने क्वांटम यांत्रिकी व्युत्पन्न किया था, कैसे हाइड्रोजन परमाणुओं से हाइड्रोजन अणुओं का गठन हुआ था, अर्थात् नाभिक A और B में केंद्रित $u_{A}$ $u_{A}$ और $u_{B}$ $u_{B}$ परमाणु हाइड्रोजन कक्ष, नीचे देखें . यह बिलकुल स्पष्ट नहीं है कि यह चुंबकत्व की ओर जाता है, लेकिन निम्न में समझाया जाएगा.

हेटलर-लंदन सिद्धांत के अनुसार, तथाकथित दो-पिंडीय आणविक $\sigma$ -कक्षों का गठन होता है, यथा परिणामी कक्षीय है:

\psi (\mathbf {r} _{1},\,\,\mathbf {r} _{2})={\frac {1}{\sqrt {2}}}\,\,\left(u_{A}(\mathbf {r} _{1})u_{B}(\mathbf {r} _{2})+u_{B}(\mathbf {r} _{1})u_{A}(\mathbf {r} _{2})\right)

यहां अंतिम उत्पाद का तात्पर्य है कि पहला इलेक्ट्रॉन, r ₁ दूसरे नाभिक में केंद्रित परमाणु हाइड्रोजन-कक्षीय में है, जबकि दूसरा इलेक्ट्रॉन पहले नाभिक आस-पास चलता है। इस "विनिमय" तत्व क्वांटम यांत्रिक गुण की अभिव्यक्ति है कि समान गुण वाले कणों की भिन्न पहचान नहीं हो सकती है। यह न केवल रासायनिक बंधन के गठन के लिए विशिष्ट है, बल्कि हम देखेंगे कि चुंबकत्व के लिए भी है, अर्थात् इस संबंध में शब्द विनिमय पारस्परिक क्रिया उत्पन्न होती है, एक शब्द जो चुंबकत्व के मूल के लिए ज़रूरी है और जो विद्युत-गतिकी द्विध्रुवीय द्विध्रुवीय पारस्परिक क्रिया से उत्पन्न होने वाली ऊर्जा से, मोटे तौर पर 100 और 1000 कारकों से भी अधिक मज़बूत है।

प्रचक्रण प्रकार्य के मामले में $\chi (s_{1},s_{2})$ , जो चुंबकत्व के लिए जिम्मेदार है, हमने पहले ही पाउली सिद्धांत का उल्लेख किया है, यथा एक सममित कक्षीय (अर्थात् ऊपर दर्शाए गए अनुसार + चिह्न द्वारा) को प्रति-सममित प्रचक्रण प्रकार्य सहित (अर्थात् - चिह्न द्वारा) गुणा करना चाहिए और इसके विपरीत . इस प्रकार:

\chi (s_{1},\,\,s_{2})={\frac {1}{\sqrt {2}}}\,\,\left(\alpha (s_{1})\beta (s_{2})-\beta (s_{1})\alpha (s_{2})\right)

,

यानी, न केवल $u_{A}$ और $u_{B}$ को, α और β द्वारा क्रमशः प्रतिस्थापित किया जाना चाहिए (प्रथम इकाई का अर्थ है "प्रचक्रण बढ़ाना", दूसरे का अर्थ है "प्रचक्रण घटाना"), बल्कि चिह्न + को - चिह्न द्वारा और अंततः r _i असतत मूल्यों द्वारा s _i(= ±½); जिससे हमारे पास हैं $\alpha (+1/2)=\beta (-1/2)=1$ और $\alpha (-1/2)=\beta (+1/2)=0$ . "एकल दशा" अर्थात् - चिह्न, यानी: प्रचक्रण प्रतिसमानांतर हैं, अर्थात् ठोस के लिए हमारे पास प्रति-लौहचुंबकत्व है और दो परमाणु अणुओं के लिए एक प्रतिचुंबकत्व है। (समध्रुवीय) रासायनिक बंधन के निर्माण की प्रवृत्ति (इसका तात्पर्य है: सममित आणविक कक्षीय का गठन, यानी + चिह्न के साथ) प्रतिसममित प्रचक्रण दशा में (अर्थात् - चिह्न के साथ) स्वतः पाउली सिद्धांत के माध्यम से परिणत होती है। इसके विपरीत, इलेक्ट्रॉनों का कूलंब विकर्षण, यानी इस विकर्षण द्वारा एक दूसरे से बचने की उनकी प्रवृत्ति, इन दो कणों के प्रतिसममित कक्षीय प्रकार्य में (अर्थात् - चिह्न सहित) और अनुपूरक सममित प्रचक्रण प्रकार्य (अर्थात् + चिह्न सहित, तथाकथित "त्रिक प्रकार्यों" में से एक) में परिणत होगी। इस प्रकार, अब प्रचक्रण समानांतर होंगे (लौहचुंबकत्व ठोस में, प्रतिचुंबकत्व दो-परमाणु गैसों में).

अंतिम उल्लिखित प्रवृत्ति लौह धातुओं, कोबाल्ट, और निकल में तथा कुछ दुर्लभ मिट्टी में हावी होती है जो लौहचुंबकीय हैं। अधिकांश अन्य धातुएं, जहां प्रथम उल्लिखित प्रवृत्ति हावी होती है, अचुंबकीय (उदा. सोडियम, एल्यूमिनियम और मैग्नीशियम) या प्रति-लौहचुंबकीय हैं (उदा. मैंगनीज़). द्विपरमाणुक गैसें भी लगभग विशेष रूप से द्विचुंबकीय हैं और प्रतिचुंबकीय नहीं। तथापि, π-कक्षीय आवेष्टन की वजह से ऑक्सीजन अणु, जीवन विज्ञान के लिए महत्वपूर्ण अपवाद है।

हेटलर-लंदन के विचारों को चुंबकत्व के हेज़नबर्ग नमूने के साथ सामान्यीकृत किया जा सकता है (हेज़नबर्ग 1928).

इस तत्व की व्याख्या इस प्रकार अनिवार्य रूप से क्वांटम यांत्रिकी की सभी बारीकियों पर आधारित है, जबकि विद्युत गतिकी मुख्य रूप से घटना-क्रिया विज्ञान को आवृत करता है।

विद्युत चुंबकत्व की इकाइयां[संपादित करें]

विद्युत चुंबकत्व से संबंधित SI इकाइयां[संपादित करें]

SI विद्युत चुंबकत्व इकाइयां
प्रतीक^[15]	मात्रा का नाम	व्युत्पन्न इकाइयां	अंतर्राष्ट्रीय से SI आधार इकाई में रूपांतरण
$\ \mathrm {I}$	विद्युत धारा	एम्पीयर (SI आधार इकाई)	$\mathrm {A=C\ s^{-1}}$
$\ Q$	विद्युत आवेश	कूलंब	$\mathrm {C=A\ s}$
$U,\ \Delta V,\ \Delta \phi ,\ \mathrm {E}$	संभावित अंतर; विद्युत वाहक का दबाव	वोल्ट	$\mathrm {V=J\ C^{-1}=kg\ A^{-1}m^{2}s^{-3}}$
$R;\ \mathrm {Z} ;\ \mathrm {X}$	विद्युत प्रतिरोध, प्रतिबाधा; प्रतिघात	ओह्म	$\mathrm {\Omega =V\ A^{-1}=kg\ m^{2}\ A^{-2}s^{-3}}$
$\ \rho$	प्रतिरोधकता	ओह्म मीटर	$\mathrm {\Omega \ m=kg\ A^{-2}m^{3}s^{-3}}$
$\ \mathrm {P}$	विद्युत शक्ति	वॉट	$\mathrm {W=V\ A=kg\ m^{2}s^{-3}}$
$\ C$	धारिता	फैरड	$\mathrm {F=C\ V^{-1}=A^{2}kg^{-1}m^{-2}s^{4}}$
$\mathbf {\mathrm {E} }$	बिजली क्षेत्र शक्ति	मीटर प्रति वोल्ट	$\mathrm {V\ m^{-1}=C^{-1}N=kg\ A^{-1}m\ s^{-3}}$
$\mathbf {D}$	बिजली विस्थापन क्षेत्र	प्रति वर्ग मीटर कूलंब	$\mathrm {C\ m^{-2}=A\ m^{-2}s}$
$\varepsilon$	विद्युतशीलता	प्रति मीटर फैरड	$\mathrm {F\ m^{-1}=A^{-2}kg^{-1}m^{-3}s^{-4}}$
$\!\chi _{e}$	बिजली सुग्राहिता	आयामरहित
$\mathrm {B} ;\ G;\ \Upsilon$	प्रवाहकत्त्व, प्रवेश्यता; सुग्राहिता	सीमेन	$\ \mathrm {S=\Omega ^{-1}=kg^{-1}A^{2}m^{-2}s^{3}}$
$\gamma ,\ \kappa ,\ \sigma$	प्रवाहकत्त्व	प्रति मीटर सीमेन	$\mathrm {S\ m^{-1}=A^{2}kg^{-1}m^{-3}s^{3}}$
$\ \mathbf {B}$	चुंबकीय प्रवाह घनत्व, चुंबकीय प्रेरण	टेस्‍ला	$\mathrm {T=Wb\ m^{-2}=kg\ A^{-1}s^{-2}}$
$\ \Phi$	चुंबकीय प्रवाह	वेबर	$\mathrm {Wb=V\ s=kg\ A^{-1}m^{2}s^{-2}}$
$\mathbf {H}$	चुंबकीय क्षेत्र शक्ति	एम्पीयर प्रति मीटर	$\mathrm {A\ m^{-1}}$
$L,\ \mathrm {M}$	प्रेरकत्व	हेनरी	$\mathrm {H=Wb\ A^{-1}=V\ A^{-1}s=kg\ A^{-2}m^{2}s^{-2}}$
$\ \mu$	पारगम्यता	हेनरी प्रति मीटर	$\mathrm {Hm^{-1}=kg\ A^{-2}m\ s^{-2}}$
$\ \chi$	चुंबकीय सुग्राहिता	आयामरहित

अन्य इकाइयां[संपादित करें]

गॉस - गॉस, संक्षिप्त रूप में G, चुंबकीय क्षेत्र (B) की CGS इकाई है।
ओर्स्टेड - ओर्स्टेड चुंबकरण क्षेत्र (H) की CGS इकाई है।
मैक्सवेल - चुंबकीय प्रवाह के लिए CGS इकाई है।
गामा - चुंबकीय प्रवाह घनत्व की एक इकाई है जोकि टेस्ला के लोकप्रिय होने से पहले आम तौर पर इस्तेमाल किया जाता था (1 गामा = 1 nT)
μ ₀ - मुक्त अंतराकाशी पारगम्यता के लिए प्रयुक्त सामान्य प्रतीक (4π×10⁻⁷ N/(एम्पियर-घूर्णन)²).

सजीव तत्व[संपादित करें]

कुछ जीव चुंबकीय क्षेत्रों का पता लगा सकता है, जो तथ्य मैगनेटोसेप्शन के रूप में जाना जाता है। चुंबकीय जैविकी चिकित्सा उपचार के रूप में चुंबकीय क्षेत्र का अध्ययन करता है; जीव द्वारा स्वाभाविक रूप से उत्पन्न क्षेत्र जैव-चुंबकत्व के रूप में जाना जाता है।

इन्हें भी देखें[संपादित करें]

विद्युत स्थैतिक
विद्युत चुंबकत्व
चुंबकीय स्थैतिक
विद्युत चुंबकत्व
लेन्ज़ क़ानून
प्लास्टिक चुंबक
चुंबक
मैग्नेटर
चुंबकीय भार
चुंबकीय शीतलन
चुंबकीय परिपथ
चुंबकीय आघूर्ण
चुंबकीय संरचना
चुंबकन
माइक्रोमैग्नेटिज्म
नियोडिमियम चुंबक
अवपीड़न
दुर्लभ-पृथ्वी चुंबक
प्रचक्रण तरंग
सहज चुंबकन
संवेदक
चुंबकीय विलोड़न
चुंबकीय क्षेत्र दृश्यमान फ़िल्म
कंपन नमूना मैग्नेटोमीटर

साँचा:Magnetic states

सन्दर्भ[संपादित करें]

↑ Oak, Purushottam Nagesh (2003). World Vedic Heritage (ebook) (Eng में). 1. New Delhi, Bharat: P. N. Oak. पृ॰ 149. Magnetism : In Vaisheshik ( 5-1-15 ) Kanaad an ancient Vedic scientist writes that a piece of iron leaps at a magnet because of an unseen force .सीएस1 रखरखाव: नामालूम भाषा (link)
↑ Fowler, Michael (1997). "Historical Beginnings of Theories of Electricity and Magnetism". मूल से 15 मार्च 2008 को पुरालेखित. अभिगमन तिथि 2008-04-02.
↑ Vowles, Hugh P. (1932). "Early Evolution of Power Engineering". Isis. University of Chicago Press. 17 (2): 412–420 [419–20]. डीओआइ:10.1086/346662.
↑ ली शू-हुआ,“Origine de la Boussole 11. Aimant et Boussole,” Isis, खंड 45, सं. 2. (जुलाई, 1954), पृ.175
↑ ली शू-हुआ, “Origine de la Boussole 11. Aimant et Boussole,” Isis, खंड 45, सं. 2. (जुलाई, 1954), पृ.176
↑ Schmidl, Petra G. (1996–1997). "Two Early Arabic Sources On The Magnetic Compass". Journal of Arabic and Islamic Studies. 1: 81–132.सीएस1 रखरखाव: तिथि प्रारूप (link)
↑ ^अ ^आ ए. आइंस्टीन: "गतिशील पिंडों के विद्युत गतिकी पर" Archived 2011-04-25 at the वेबैक मशीन, 30 जून 1905.
↑ B. D. Cullity, C. D. Graham (2008). Introduction to Magnetic Materials (2 संस्करण). Wiley-IEEE. पृ॰ 103. आई॰ऍस॰बी॰ऍन॰ 0471477419.
↑ [15]
↑ Catherine Westbrook, Carolyn Kaut, Carolyn Kaut-Roth (1998). MRI (Magnetic Resonance Imaging) in practice (2 संस्करण). Wiley-Blackwell. पृ॰ 217. आई॰ऍस॰बी॰ऍन॰ 0632042052.सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)
↑ Griffiths, David J. (1998). Introduction to Electrodynamics (3rd संस्करण). Prentice Hall. OCLC 40251748. आई॰ऍस॰बी॰ऍन॰ 0-13-805326-X. मूल से 11 जून 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019., अध्याय 12
↑ Jackson, John David (1999). Classical electrodynamics (3rd संस्करण). New York, [NY.]: Wiley. आई॰ऍस॰बी॰ऍन॰ 0-471-30932-X. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.
↑ मिल्टन द्वारा कुछ अनिर्णायक घटनाओं का उल्लेख (पृ.60) और फिर भी निष्कर्ष निकाला कि "चुंबकीय एकलध्रुवों के बचने के कोई सबूत मौजूद नहीं" (पृ.3). Milton, Kimball A. (2006). "Theoretical and experimental status of magnetic monopoles". Reports on Progress in Physics. 69 (6): 1637–1711. arXiv:hep-ex/0602040. डीओआइ:10.1088/0034-4885/69/6/R02. नामालूम प्राचल |month= की उपेक्षा की गयी (मदद) .
↑ Guth, Alan (1997). The Inflationary Universe: The Quest for a New Theory of Cosmic Origins. Perseus. OCLC 38941224. आई॰ऍस॰बी॰ऍन॰ 0-201-32840-2. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019. .
↑ साँचा:GreenBookRef2nd

नोट

Furlani, Edward P. (2001). Permanent Magnet and Electromechanical Devices: Materials, Analysis and Applications. Academic Press. OCLC 162129430. आई॰ऍस॰बी॰ऍन॰ 0-12-269951-3. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.
Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. OCLC 40251748. आई॰ऍस॰बी॰ऍन॰ 0-13-805326-X. मूल से 11 जून 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.
Kronmüller, Helmut. (2007). Handbook of Magnetism and Advanced Magnetic Materials, 5 Volume Set. John Wiley & Sons. OCLC 124165851. आई॰ऍस॰बी॰ऍन॰ 978-0-470-02217-7. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.
Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. OCLC 51095685. आई॰ऍस॰बी॰ऍन॰ 0-7167-0810-8. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.
David K. Cheng (1992). Field and Wave Electromagnetics. Addison-Wesley Publishing Company, Inc. आई॰ऍस॰बी॰ऍन॰ 0-201-12819-5. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.

बाहरी कड़ियाँ[संपादित करें]

विकिपुस्तक पर

School science how-to से सम्बन्धित एक किताब है।

चुंबकत्व को विक्षनरी में देखें जो एक मुक्त शब्दकोश है।

बीबीसी के इन आवर टाइम में Magnetism। (अभी सुनें)
चुंबकत्व प्रयोग Archived 2011-07-16 at the वेबैक मशीन
विद्युत चुंबकत्व - ऑनलाइन पाठ्यपुस्तक से एक अध्याय
चुंबकत्व के बारे में जेकोब बोगाटिन
वीडियो: भौतिक विज्ञानी रिचर्ड फेनमैन द्वारा सवालों के जवाब, बार मैग्नेट एक दूसरे के प्रति आकर्षित या विकर्षित होते हैं?
चुंबक पर, 1600 इलेक्ट्रिकल इंजीनियरिंग के जनक द्वारा चुंबकत्व पर सर्वप्रथम पुस्तक. पूरा अंग्रेजी पाठ, पूर्ण पाठ खोज.

[1] Oak, Purushottam Nagesh (2003). World Vedic Heritage (ebook) (Eng में). 1. New Delhi, Bharat: P. N. Oak. पृ॰ 149. Magnetism : In Vaisheshik ( 5-1-15 ) Kanaad an ancient Vedic scientist writes that a piece of iron leaps at a magnet because of an unseen force .सीएस1 रखरखाव: नामालूम भाषा (link)

[2] Fowler, Michael (1997). "Historical Beginnings of Theories of Electricity and Magnetism". मूल से 15 मार्च 2008 को पुरालेखित. अभिगमन तिथि 2008-04-02.

[3] Vowles, Hugh P. (1932). "Early Evolution of Power Engineering". Isis. University of Chicago Press. 17 (2): 412–420 [419–20]. डीओआइ:10.1086/346662.

[4] ली शू-हुआ,“Origine de la Boussole 11. Aimant et Boussole,” Isis, खंड 45, सं. 2. (जुलाई, 1954), पृ.175

[5] ली शू-हुआ, “Origine de la Boussole 11. Aimant et Boussole,” Isis, खंड 45, सं. 2. (जुलाई, 1954), पृ.176

[6] Schmidl, Petra G. (1996–1997). "Two Early Arabic Sources On The Magnetic Compass". Journal of Arabic and Islamic Studies. 1: 81–132.सीएस1 रखरखाव: तिथि प्रारूप (link)

[Moving-7] अ ^आ ए. आइंस्टीन: "गतिशील पिंडों के विद्युत गतिकी पर" Archived 2011-04-25 at the वेबैक मशीन, 30 जून 1905.

[Graham-8] B. D. Cullity, C. D. Graham (2008). Introduction to Magnetic Materials (2 संस्करण). Wiley-IEEE. पृ॰ 103. आई॰ऍस॰बी॰ऍन॰ 0471477419.

[Meyers1-9] [15]

[Westbrook-10] Catherine Westbrook, Carolyn Kaut, Carolyn Kaut-Roth (1998). MRI (Magnetic Resonance Imaging) in practice (2 संस्करण). Wiley-Blackwell. पृ॰ 217. आई॰ऍस॰बी॰ऍन॰ 0632042052.सीएस1 रखरखाव: एक से अधिक नाम: authors list (link)

[11] Griffiths, David J. (1998). Introduction to Electrodynamics (3rd संस्करण). Prentice Hall. OCLC 40251748. आई॰ऍस॰बी॰ऍन॰ 0-13-805326-X. मूल से 11 जून 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019., अध्याय 12

[12] Jackson, John David (1999). Classical electrodynamics (3rd संस्करण). New York, [NY.]: Wiley. आई॰ऍस॰बी॰ऍन॰ 0-471-30932-X. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019.

[13] मिल्टन द्वारा कुछ अनिर्णायक घटनाओं का उल्लेख (पृ.60) और फिर भी निष्कर्ष निकाला कि "चुंबकीय एकलध्रुवों के बचने के कोई सबूत मौजूद नहीं" (पृ.3). Milton, Kimball A. (2006). "Theoretical and experimental status of magnetic monopoles". Reports on Progress in Physics. 69 (6): 1637–1711. arXiv:hep-ex/0602040. डीओआइ:10.1088/0034-4885/69/6/R02. नामालूम प्राचल |month= की उपेक्षा की गयी (मदद) .

[14] Guth, Alan (1997). The Inflationary Universe: The Quest for a New Theory of Cosmic Origins. Perseus. OCLC 38941224. आई॰ऍस॰बी॰ऍन॰ 0-201-32840-2. मूल से 2 अक्तूबर 2019 को पुरालेखित. अभिगमन तिथि 23 अक्तूबर 2019. .

[15] साँचा:GreenBookRef2nd

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]