क्षेत्रफल का द्वितीय आघूर्ण
क्षेत्रफल का द्वितीय आघूर्ण (second moment of area) किसी क्षेत्र का एक ज्यामितीय गुण है जो यह दर्शाता है कि उस क्षेत्र के बिन्दु किसी अक्ष के सापेक्ष किस प्रकार की स्थिति में हैं। इसे प्रायः या से निरूपित करते हैं। इसकी विमा, L4 है।
संरचना इंजीनियरी के क्षेत्र में क्षेत्रफल के द्वितीय आघूर्ण का बहुत उपयोग होता है। किसी धरन (बीम) के अनुप्रस्थ काट के क्षेत्रफल का द्वितीय आघूर्ण उस धरन की एक महत्वपूर्ण गुण है जो लोड के कारण उस बीम के विक्षेप (deflection) के परिकलन में प्रयुक्त होता है।
परिभाषा[संपादित करें]
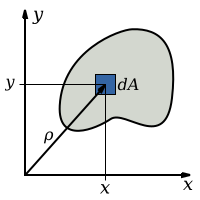
किसी क्षेत्रफल का किसी अक्ष के सापेक्ष द्वितीय आघूर्ण निम्नवत परिभाषित है-
जहाँ
- = अतिसूक्ष्म क्षेत्रफल है
- = अक्ष BB से dA की दूरी
उदाहरण के लिए, यदि x-अक्ष के सापेक्ष क्षेत्रफल का द्वितीय आघूर्ण निकालना हो तो, (प्रायः से निरूपित) की गणना कार्तीय निर्देशांक में इस प्रकार की जा सकती है:
उदाहरण[संपादित करें]
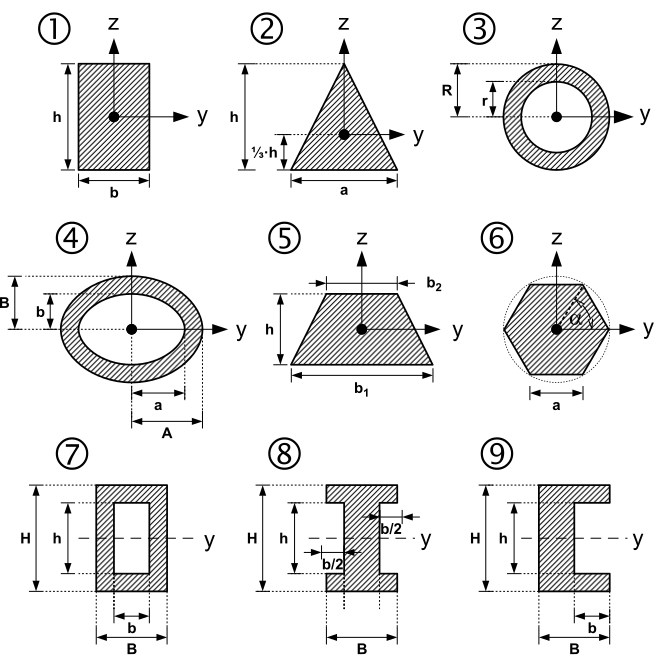
क्षेत्रफल का द्वितीय आघूर्ण , बशर्ते इसकी सन्दर्भ-अक्ष y-अक्ष अथा z-अक्ष के कटान बिन्दु से होकर जाये।
| क्रमांक | क्षेत्रफल | y- और z-अक्ष के सापेक्ष क्षेत्रफल का द्वितीय आघूर्ण |
टिप्पणी |
|---|---|---|---|
| 1: आयत |
|
वर्ग के लिये | |
| 2:त्रिभुज |
|
त्रिभुज केवल z-अक्ष के प्रति सममित होता है। | |
| 3:वलय | पूर्ण वृत्त के लिये | ||
| 4:दीर्घवृत्ताकार वलय |
|
||
| 5: सममित समलम्ब चतुर्भुज |
| ||
| 6: सम n-भुज | सभी अक्षों के प्रति सममित है। | ||
| 7: आयताकार फ्रेम |
-(केवल चित्र 7 के लिये लागू ; अन्य सूत्र, चित्र 8 और 9 के लिये लागू होते हैं | ||
| 8: आई-सेक्सन | |||
| 9: C-सेक्शन |
अन्य उदाहरण (इंजीनियरिंग विश्वकोश से)



































