उच्चिष्ठ और निम्निष्ठ
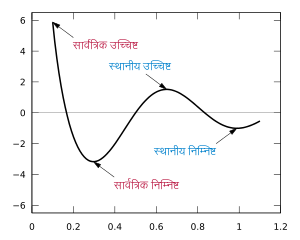
गणित में किसी फलन के सबसे अधिक और सबसे कम मान को उस फलन का उच्चिष्ट और निम्निष्ट (maximum and minimum ; बहुवचन : maxima and minima) कहते हैं। उच्चिष्ट और निम्निष्ट को सम्मिलित रूप से चरम (extrema ; एकवचन: extremum) कहते हैं। ये उच्चिष्ट और निम्निष्ट फलन के किसी सीमित क्षेत्र में हो सकते हैं अथवा उस फलन के सम्पूर्ण डोमेन में। फलन के किसी सीमित क्षेत्र में स्थित उच्चिष्ट और निम्निष्ट को 'स्थानीय चरम' (local or relative extremum) कहते हैं जबकि फलन के सम्पूर्ण डोमेन में फलन का जो सबसे अधिक/कम मान हो उसे 'ग्लोबल चरम' (global or absolute extremum) कहते हैं। पार्श्व चित्र में लोबल और लोकल चरम मान दिखाये गये हैं।
इससे अधिक व्यापक रूप से कहें तो, किसी समुच्चय का उच्चिष्ट और निम्निष्ट, उस समुच्चय के सदस्यों में सबसे अधिक और सबसे कम मान वाले सदस्य होते हैं।
फलनों के चरम मानों को निकालना ही इष्टतमकरण (optimization) का उद्देश्य है।
उच्चिष्ट और निम्निष्ट का परिकलन[संपादित करें]
उदाहरण (१)[संपादित करें]
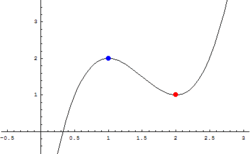
हम निम्नलिखित फलन पर विचार करते हैं (सामने इस फलन के ग्राफ को देखें)
- .
सबसे पहले हम इस फलन का प्रथम अवकलज निकालते हैं और उसको शून्य (0) के बराबर रखकर सम्भावित उच्चिष्ट/निम्निष्ट का पता लगाते हैं।
इस बात को सुनिश्चित करने के लिये कि x = 0 पर उच्चिष्ट/निम्निष्ट है, हम इस x=0 पर इस फलन के द्वितीय अवकलज का मान निकालते हैं और देखते हैं कि दोनों बिन्दुओं (x = 1 तथा x = 2) पर द्वितीय अवकलज धनात्मक है या ऋणात्मक।
- उच्चिष्ट (नीला बिन्दु)
- निम्निष्ट (लाल बिन्दु)
उदाहरण (२)[संपादित करें]
निम्नलिखित फलन को लेते हैं-
- .
इसका प्रथम अवकलज निकालते हैं:
फलन का द्वितीय अवकलज यह है:
प्रथम अवकलज को शून्य (0) रखने पर x का मान निम्नलिखित मिलता है-
पर फलन के द्वितीय अवकलज का मान ऋणात्मक है, अतः x=x_1 पर इस फलन का उच्चिष्ट है।
इसी प्रकार हम देखते हैं कि पर फलन के द्वितीय अवकलज का मान धनात्मक है, अतः x_2 पर फलन का निम्निष्ट है।
उदाहरण (३)[संपादित करें]

निम्नलिखित फलन पर विचार करें जिसका ग्राफ सामने दिया गया है-
- .
सबसे पहले हम इस फलन का प्रथम अवकलज निकालते हैं और उसको शून्य के बराबर रखकर सम्भावित उच्चिष्ट/निम्निष्ट का पता लगाते हैं।
इस बात को सुनिश्चित करने के लिये कि x = 0 पर उच्चिष्ट/निम्निष्ट है, हम इस x=0 पर इस फलन के द्वितीय अवकलज का मान निकालते हैं और देखते हैं कि यह धनात्मक है या ऋणात्मक।
- उच्चिष्ट या निम्निष्ट दोनों नहीं हैं बल्कि यह इन्फ्लेक्शन बिन्दु है। (चित्र में हरा बिन्दु)
अतः हम निष्कर्ष निकालते हैं कि इस फलन का कोई न उच्चिष्ट है न कोई निम्निष्ट।
कुछ ध्यान देने योग्य बातें[संपादित करें]

- फलन x2 का एकमात्र ग्लोबल मिनिमम है जो x = 0 पर है।
- फलन x3 का कोई भी ग्लोबल मिनिमा या मैक्सिमा नहीं है। यद्यपि इसके प्रथम अवकलज (3x2) का मान x = 0 पर 0 है किन्तु यह एक inflection point है न कि उच्चिष्ट या निम्निष्ट।
- फलन का एक यूनिक ग्लोबल मैक्सिमा x = e पर है। (सामने के चित्र को देखिये)
- The function x-x has a unique global maximum over the positive real numbers at x = 1/e.
- The function x3/3 − x has first derivative x2 − 1 and second derivative 2x. Setting the first derivative to 0 and solving for x gives stationary points at −1 and +1. From the sign of the second derivative we can see that −1 is a local maximum and +1 is a local minimum. Note that this function has no global maximum or minimum.
- The function |x| has a global minimum at x = 0 that cannot be found by taking derivatives, because the derivative does not exist at x = 0.
- The function cos(x) has infinitely many global maxima at 0, ±2π, ±4π, …, and infinitely many global minima at ±π, ±3π, ….
- The function 2 cos(x) − x has infinitely many local maxima and minima, but no global maximum or minimum.
- The function cos(3πx)/x with 0.1 ≤ x ≤ 1.1 has a global maximum at x = 0.1 (a boundary), a global minimum near x = 0.3, a local maximum near x = 0.6, and a local minimum near x = 1.0. (See figure at top of page.)
- The function x3 + 3x2 − 2x + 1 defined over the closed interval (segment) [−4,2] has a local maximum at x = −1−√15⁄3, a local minimum at x = −1+√15⁄3, a global maximum at x = 2 and a global minimum at x = −4.
इन्हें भी देखें[संपादित करें]
- रॉल प्रमेय (Rolle's theorem)
बाहरी कड़ियाँ[संपादित करें]
- Maxima and Minima From MathWorld--A Wolfram Web Resource.
- Thomas Simpson's work on Maxima and Minima at Convergence
- Application of Maxima and Minima with sub pages of solved problems
















![{\displaystyle {\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b4a0a76158849854a302fc639dfc882ec16008)